※すなわち、オブジェクト指向(object oriented)である(オブジェクト指向のコンセプトはデジタル化の核・本質をなす、超偉大な発明である)!もちろん医療のデジタル化(医デジ化:Me-DigIT)においてもプログラムによって構築・拡大されるデジタルな医療の世界をあたかも工場におけるプラントのようなアナログ的機能構造物の集合(体)として直観的・幾何学・野性的に捉え、これをハンドリングできるようにしようとするオブジェクト指向の精神・考え方がその土台・土俵・インフラストラクチャ(基盤)となっている。オブジェクト指向(object oriented)は『Smalltalk』を開発したゼロックス社パロアルト研究所の計算機科学者アラン・ケイがプログラミング言語『Simula(SIMUlation LAnguage)』に大いに感化されて大学院時代に日夜プログラミング・アーキテクチャの思索(しさく)に耽(ふけ)っていた1967年頃、『今何をしているのか?』と尋ねられて『object-oriented programmingだよ!』と答えたのがその起点・原点・出発点・一丁目一番地であるといわれている。いったんデジタルに機能関数群ベクトルとして構造化することができればそのデジタル化機能関数群構造物をコネコネとたしひきかけわりおよびその極限たる微分・積分によってトランスフォームすることも自由自在である。
(設定)パラメータ(parameter)とはロールプレイングゲームにおける新規キャラクター生成時の知力、体力、(時の)運、魔法力といった能力属性(property)や値の付与・設定など、特定の関数(処理、ここではキャラクターの生成関数)が実行されるごとに属性や値が付与・設定されるその(設定)変数(variable)といったくらいの意味合いである。
パラメータの一般・典型・代表的な使い方(考え方)として、(たとえば面(体積)積分の計算を遂行するときや、全微分を偏微分の(1次線形)和に分離・分割するときなど)考慮すべきパラメータが複数ある場合には、(あたかも)1つのパラメータのみが(ある値からある値へと)動くものと(仮定)して、そのほかのパラメータについては(その間、あたかも)ある値に(静的に)固定された定数であるかのごとく(仮定して)扱ってこれを計算しようという技巧(ぎこう)的なものがある。
これにより1つのパラメータの解析が終わったあとに、動きのあるパラメータを順々に切り替えてゆくことができ、首尾(しゅび)よく計算を遂行することができる。なぜこのようなまわりくどい考え方をするのかというと『田口メソッド(なんらかのパラメータ解析をするときには、こんがらがってしまうのでパラメータを2つ同時には動かさないようにしようとする(きわめて泥臭い、人間的な!)方法)』よろしく人間は複数の動きのあるパラメータを同時に扱うことが苦手であるから、(人間は1次線形性を仮定して)これを首尾よく各個撃破(かっこげきは)したいのである(2兎を(同時に!)追うものは1兎をも得ず!である!)。
関数の性質・属性(property)のうち最も本質的なものとして考慮されるべきものは、まずはその微分(可能性)および積分(可能性)であろう。これを踏まえて『解析的な関数※』とは、有界かつ有限の区間の外では値がゼロ(という意味でコンパクト※※、すなわち積分値も有限の値をもつ、換言すれば発散しないこと)であり、なおかつ何度でも(無限回!)微分ができる(値の増減傾向(1次近似)が調ベられる)ような関数※※※であるとして定義されるのが一般・典型・代表的のようである。
※使われる文脈にもよるものだろうが、ほかにx=αでテイラー(あるいはその一般化拡張としてのローラン)展開★できる(したがって、何度でも(無限回!)微分ができ、値の増減傾向(1次近似)が調ベられる!)という定義もある。
※※(有界な!)閉区間の一般化(数直線上では上限と下限を区間内にもつということ)であるコンパクト性はε-δ論法よろしく、数学的初学者にとって理解が最も難しい概念のひとつである。コンパクト性は連続写像に対して常に保存される(したがって、とりわけ伸縮をともなって柔軟に変形する幾何学(トポロジー)において何らかの物体(多様体:たようたい)の構図・構造およびその変形(変形前後の点と点との1対1の対応関係)を捉えるうえではこの概念なしにはおよそ有効な議論を展開することなどできはしない!)。また、このことが増減傾向を調べたり(解析)や体積を求めたり(計量)することをその本分とする微分・積分学においてもその基礎・基盤・土台・土俵・インフラストラクチャになっている。
開区間のように見かけ上は有限であるものの、両端がない(あるいは『両端に開球(という余計なモノ!?)がくっついてしまっている!』という捉え方もできる!※)おかげで実は無限区間と一対一※の対応がついてしまう性質(同相)のものと閉区間のように両端がある(閉球がくっついている)がために本質的に有限の範疇にとどまっており、無限区間との一対一の対応がどうしてもとることができない性質(非同相)のものとは似て非なる概念として厳密に区別されるべきものであることに注意されたい。
※『麺(めん)を打つ際に生地を引き伸(の)ばす名人』がごとく、開区間は無限区間と一対一に対応している(全単射)。全射(全体の領域を全体の領域に写す)かつ単射(入力が異なれば出力も異なる)であることを全単射(ぜんたんしゃ)であるという。
与えられたいかなる被覆セットに対してもかならず、有限個の開球バブル(ここでは有限個でありさえすれば無限に大きな径のバブルを用いても一向に構わない!ものとする)の被覆セットを選択できる。開区間は閉区間の場合とは異なり、たとえ有界な区間であったとしても(その端点に開球(かいきゅう)バブルを配置することができない(開区間のなかに極大元あるいは極小元をもたない))というただその1点において、どうしてもその端点において(延々・脈々・累々とつづく後出しジャンケンのチキンレースをするがごとく、より端っこを選択されてしまうという!)無限(性)をはらんでしまう(その選択の無限性を排除することができない!)がためにコンパクトであるとはいくら悔しがっても言うことができない。
具体的にたとえば(無限級数の極限値(集積点:cluster point)たる!)端点付近で開球バブルの中心が無限級数の列となるように配置された無限個の開球バブルによる被覆パターンが構成されてしまっているような場合、これらから被覆が破綻(はたん)してしまわないような有限個の開球バブル(ここでは有限個でありさえすれば無限に大きな径のバブルを用いても一向に構わない!ものとする)の被覆セットを選択することは(いくら悔しがっても!)できない。すなわち有限個の開球のバブルのみではどうしても(点ではなく区間レベルの!隙間のある)穴があいてしまい、いくら悔しがってみたところで(この区間の穴から)被覆が破綻して泡のごとくはかなく消えてしまう被覆パターンがどうしても排除しきれずに残存してしまう(すなわち、コンパクトであるとはいくら悔しがっても言うことができない)のだ。
※ひとつの複素数入力値zに対して、複数(N個)の複素数出力値をもつ関数を(複素)多(N)価関数と呼ぶ(複素関数は多入力多出力系(通常は2入力2出力)あるいはベクトル入力ベクトル出力系の枠組みのなかで捉えるほうが今日(こんにち)では深層学習や生成AIとも関連してより包括的でスッキリと捉(とら)えられるかもしれない、、、)。
複素関数を考える効用としてほかにも、実数領域においては2コバラバラに捉えられてきた三角関数と指数関数とがオイラーの公式によって複素数領域においては2コイチで結びついていると捉えられることがあげられる(複素関数は多入力多出力系(通常は2入力2出力)あるいはベクトル入力ベクトル出力系の枠組み(フレーム)のなかで捉えるほうが深層学習や生成AIとも関連してより包括的でスッキリとするかもしれない、、、)。このように実関数を普遍・一般・抽象化したメタ的な概念である複素関数という枠組み(フレーム)のなかで考えることによって(従来バラバラに捉えられてきた数学的概念における)さまざまなコミュニケーション・リンク(およびそこで働く超偉大なるテンション(超万有引力!))が顕在化(けんざいか)し、にわかに数式が輝き、躍動し始めるのである!(同じ現象を捉えるにしても単眼(たんがん)ではなく複眼(ふくがん)、さらには多眼(たがん)という枠組み(フレーム)のなかで捉えることによって今までとは大きく、世界は違って(変わって、異なって)見えてくるというのである!)
オイラーの公式
特に、θ = π のとき

となり、この関係はオイラーの恒等式(Euler's identity)と呼ばれる。
グルサ(Goursat)の定理は複素積分においては極の値を変数とみてコーシーの積分公式の両辺を微分することによって簡便に導かれる。コーシーの積分公式の見た目は一見いかつくて、気軽に扱えないような、如何(いか)にも近寄りがたい空(雰囲)気(atmosphere)を醸(かも)し出してくるが(だまされてはいけない!)、その全体的構図(構造、状況、ゲシュタルト)とその意味するところを一旦わかってしまえば、世界は違って見えてくる!実は驚くほどシンプルかつ簡便・有用な公式である!
余談だが、当てようとおもってもなかなか狙(ねら)い通りに当たらないが、読書百遍義自ずから顕る(どくしょひゃっぺんぎおのずからあらわる)!ぐるぐるとブラッシュアップし(締(し)め上げ)ながら出し続けていると気づかぬうちに、特異点を左回りでぐるぐる巻きに周回しており(Get the Me-DigIT HARVEST !!!!)、思わぬところで当たることになるというのが申請書申請の真骨頂(しんこっちよう、就活や入試勉強も同様か!?)。そういう、セレンディピティの効果に期待する心持(こころもち)が今後ますます重要になってくるかとおもわれます。
すなわち、もちろん当たるのが目的なんだけど、実際に当たる確率が相当(そうとう)に低い場合には統制的目標あるいは制御点として(恋文(こいぶみ)よろしく!ぐるぐる巻きに)出し続け(られ)ること(結果ではなく!行(運)動戦略目標の設定による慣性力(モチベーションの維持力)!の向上)が重要な行(運)動戦略目標になってくる、、、おそらく(その間に留数値~Me-DigIT HARVESTがたまって)江戸の敵を(結果的に)長崎で討つみたいに別の財団への申請で思いがけずあたるということになりそう、、、審査員が興味をもってくれれば多少の反応くらいはあるかも、、、(結果ではなく!行(運)動戦略目標設定による慣性力向上法)
Get the Me-DigIT ROLLING, ROLLING, AND ROLLING !!!(われわれの場合)
(参考文献)
馬場敬之,常微分方程式,マセマ出版社.
上記のインパルス関数(ディラックのδ(デルタ)関数とも呼ばれる)は『あらゆる出来事(accident)のその瞬間その瞬間を切り取って(cut out)、これを抽出(析出:せきしゅつ)』せしめることから、その二つ名(ふたつな)を『ドラえもんの世界の関数』ともいう。英国の物理学者であるディラック(1902-84)は量子力学の研究の最中(さなか)にこの関数を発見・導入し、議論を単純・明解に進めることに成功した。
ディラックの功績として他にもMRIでも用いられている『ポジトロン(陽電子)』の予言や『磁気モノポール(単極子)』の提唱(素粒子としてはまだ発見されていない。宇宙のインフレーションの名残(なごり)として生み出されたと仮定されるものの一つであり、スーパーカミオカンデなどで磁気モノポールを観測する試みが現在も続けられている。)がよく知られている。
ちなみに複素関数論においてもディラックのデルタ関数とまるで双子のように瓜(うり)二つの特長をもつ抽出関数が現れる。コーシーの積分公式とよばれる(その二つ名は『ドラミちゃんの関数』といったところか)。コーシーの積分公式の見た目は一見いかつくて、気軽に扱えないような、如何(いか)にも近寄りがたい空気を醸(かも)し出してくるが(だまされてはいけない!)、その全体的構図(構造、状況、ゲシュタルト)とその意味するところを一旦わかってしまえば、世界は違って見えてくる!驚くほどシンプルかつ簡便・有用な公式である。
具体的に投げ縄の輪を締め上げるように積分路Cを特異点z=a(極)のまわりに極限までぐるぐる巻きに締め上げて縮小すると、f(z)はもうほとんど定数f(a)として扱える(微分による1次線形近似と同様の考え方である!局所的には Me-DigIT!定数f(a)があらわれる(析出(せきしゅつ)される)!)ことをコーシーの積分公式は率直に表現している。
このようにコーシーの積分公式は特異点(極)まわりに積分路をぐるぐる巻きに締め上げるとそこでの経路に沿った関数の(複素)積分値を(あたかもHarvest(天の恵みがもたらす収穫(成果)量)たる!)や何かしらのありがたい結晶がごとく!留数として)析出(せきしゅつ)せしめる。この考え方(イメージ、感覚)はきわめて示唆(しさ)と拡張性(かくちょうせい)に富んでおり、人工知能援用医療ロボット工学、医用画像工学においてもきわめて応用の効く、有用なものの観方、考え方、捉え方、発想の仕方、世界観をもたらす!
すなわち変形をともなって運動する臓器内に埋め込まれた患部(腫瘍や結石)を包含(ほうがん)するように関心領域(積分路C)をうまく抽出(われわれはこれを、ディラックのデルタ関数、コーシーの積分公式につづく、第3の(スーパー)抽出関数として(われわれは敬意をこめてこれを)『Me-DigIT Harvest 抽出関数』と呼ぼう!)・追従しながらバウンディング・ボックスなどを用いて捉え、これをぐるぐる巻きに締め上げてゆければ、あたかも静的(static)な世界でピン止め・ピンフォール(抑え込み)固定したかのように患部を扱うことができ、診断や治療におけるモニタリングを容易化することに大いに役立てることができる!※※この場合、運動する臓器内に埋め込まれた患部(腫瘍や結石)の大きさ(や広がり)といった診断・治療において有用な特徴量が留数(われわれはこれをMe-DigIT Harvest!と呼ぼう)に対応しており、われわれMe-DigITプロジェクトでは世界有数の腕利きのMe-Digistar(メディジスター※)たちがただこれを得たいがために集(つど)い、あーでもない、こうでもないと言いながら日夜モニタやロボットを前にして苦心(くしん)して奮闘(ふんとう)・格闘(かくとう)しているのである。
※メディジスター(Me-Digistar)のネーミングにあたり、お医者さん(Doctor)とトランジスタ(Transistor)とを参考にした(ただし、超新星(Supernova)とかけて語尾を『stor』ではなく『star』としている)。トランジスタとは、電気の流れをコントロールする電子部品で、多くの電子回路で頻回に用いられている。 電気信号を大きくする増幅機能と、電気を流したり止めたりするスイッチング・コントロール機能とがある。 今日では、スマートフォン、パソコン、テレビなど、身近にある日常的に使っている電化製品のほとんど全てにおいてトランジスタは用いられている。
※※これを実現する方法には深層学習を用いたさまざまな高精度な型抜き(Segmentation)手法が提案されてきているが、深層学習を用いない直観的かつトポロジカルで先駆的な古典的手法の代表的なものとしてエネルギー関数を定義して、蛇のようにぐるぐると輪郭を締め上げてゆく動的輪郭法(スネーク法)が知られている。
現実の物理現象としては電磁気学におけるアンペールの法則(およびビオサバールの公式)が, 複素解析におけるコーシーの積分公式(および留数定理※)に対応している。具体的にコーシーの積分公式の左辺(に2πiを乗じたもの)が電流値、右辺(を2πiで割ったもの)が磁界(場)の経路積分に対応する。
※複素積分の値が簡便に得られる。留数定理においては『(2位でもダメで、)選ばれし1位の極(star)のみ、留(とど)め置かれ(て残りはすべて掃(は)け)る』という、大変厳しいセレクションがかかる。
(参考文献)
岩下弘一,工科のための複素積分,数理工学者.p91の『複素積分の物理的意味』の項の解説が直観的に大変明解で大変参考になる.
(複素積分において)特異点を左手に見て(関心領域内に特異点を包含して)積分する(ぐるぐる巻きに巻き上げる)か、右手に見て(関心領域内に特異点を包含しないで)積分する(逆方向に巻き戻す:負の方向に巻き上げるという見方もある!)かとは似て非なることであり、得られる(Me-DigIT!)果実(Harvest、計算結果)は大きく変わってきてしまうのである(複素関数の多価(たか)性の原因、リーマン面を想起せよ!)!患部を臓器内に包含しながら巻き上げるのか、包含しないように逆方向に巻き戻すのか?包含する場合、(孤立特異点的であってMe-DigIT Harvestとして)摘出して完全に除去することは可能なのか?それが問題である!
(参考文献)
Joonho Seo, Norihiro Koizumi, Takakazu Funamoto, Naohiko Sugita, Kiyoshi Yoshinaka, Akira Nomiya, Akira Ishikawa, Yukio Homma, Yoichiro Matsumoto, and Mamoru Mitsuishi, " Visual Servoing for a US-guided therapeutic HIFU system by coagulated lesion tracking: a phantom study," International Journal of Medical Robotics and Computer Assisted Surgery (IJMRCAS), Vol.7, pp.237-247, https://doi.org/10.1002/rcs.394, 2011.
A. Mariani, L. Morchi, A. Diodato, S. Tognarelli and A. Menciassi, "High-Intensity Focused Ultrasound Surgery Based on KUKA Robot: A Computer-Assisted Platform for Noninvasive Surgical Treatments on Static and Moving Organs," IEEE Robotics & Automation Magazine, vol. 30, no. 3, pp. 79-93, Sept. 2023, https://doi.org/10.1109/MRA.2022.3188221.
インパルス関数を積分したものは、(ヘヴィサイドの)ステップ関数で、スイッチを入れたときのような値の振る舞い(変化)をすることから、その二つ名を名付けるならば『スイッチ・オン関数』とでも呼ぶべきものであろう。ここで、ディラックのδ(i-j)関数が19世紀のドイツの数学者レオポルト・クロネッカーが発見したクロネッカーのδij関数の添え字(インデックス)i,jの自然数(離散)から実数(連続)へのメタ的拡張になっている点も見逃せない。
※呼び名について、転置をとるごとに自身に(-1)をかけた値になる(正負の符号が交代する)行列を交代行列(こうたいぎょうれつ、alternating matrix)と呼び、その二つ名を歪対称行列(わい・ひずみたいしょうぎょうれつ、skew-symmetric matrix)と呼ぶこともある。歪対称行列の『歪(わい・ひずみ)』という文字は1回転置をとると成分に−1(負)をかけた(符号が交代した)値になり、もう1回転置をとるともとの値(正)にもどることを(苦心して!)うまく体現(たいげん)していると思う。
交代行列には三つ名(みつな)もあって反対称行列(はんたいしょうぎょうれつ、antisymmetric matrix)と呼ばれることもある。交代行列の複素拡張である反(はん)エルミート行列との対応においては、反対称行列という呼び名が一番相応(そうおう)であると言えるだろう。
交代行列は(一般・典型・代表的には)原点を中心とする微小面積要素(領域)の(瞬間)(ねじり)回転(変形運動)力(モーメント、トルク)をあらわし、微小(矩形であらわすことが一般・典型・代表的な)領域(コントロール・ボリューム)に対して(あくまで!)局所的なせん断ひずみをもたらす(さきほどの歪対称行列の『歪(わい・ひずみ)』の由来となっている)。
(一般・典型・代表的な)はりのたわみの例で(具体的に!)考えるとまずは因果関係(いんがかんけい)として、はりに加わった対となっている(2コイチ)の荷重(力)やモーメントを原因とする結果として、はりにたわみが生じている。ここで、このたわみの量に応じて(受動的に!)生み出される反力・反モーメントとはりに加わった荷重(力)やモーメントとの間には(2コイチの)作用・反作用の(因果)関係が(あくまで!)局所的(なコントロール・ボリューム内)に存在していることに着目されたい。
この(あくまで!)局所的な(2コイチの)作用・反作用の関係によってはりの内部のコントロール・ボリュームにおいて今まさに、対向(たいこう)する方向に、ギシギシときしみ音(おん)を立てながらつり合い、(2コイチで)互(たが)いに打ち消しあっている単位面積(要素)あたりの(あくまで!)局所的な内力(ないりょく)としての(応)力や(応)モーメントこそがせん断(応)力、曲げモーメントの正体(Identity)なのである。
ひずみ対称行列において対角線を挟(はさ)んで正負の符号が入れ替わっているのは今まさにこの(はりの内部の)コントロール・ボリュームにおいてギシギシときしみ音(おん)を立てながらつり合って(あくまで!)局所的に(見合って)いる状態を率直に表現している※(率直な数学的表現が物理の本質を垣間見せる好例と言えよう)。
※正確には、ひずみ対称行列の各行はダランベールの原理よろしくまさしく、材料力学の指導原理といって然(しか)るべきものであり、2組の対となっている(2コイチの)偶力(ぐうりょく)・応力の片割れどうし(F_xとF_y)が内力(ないりょく)として対向しながら、曲げモーメント(2コイチの偶モーメント、応モーメント)としては(あくまで!)局所的につりあっている状態を如実(にょじつ)に表(体)現し、これは(曲げモーメント(2コイチの応モーメント)としてはつり合いながらも)コントロール・ボリュームにせん断ひずみ(たわみ角)とよばれる(あくまで!)局所的な変形をもたらしている(これを空間で積分すれば大域的なはりのたわみ(変形)を計算できる)。このとき偶力・応力を構成する対となる(2コイチ)の対向する内力(片割れの対、r_y F_xと-r_y F_x、r_x F_yと-r_x F_yといった対向してつり合うモーメントの対)の構図・構造はひずみ対称行列において対角線を挟(はさ)んで正負の符号が入れ替わった状態でお互いに対峙(たいじ)してギシギシというきしみ音とともににらみ合っていることでうまく表(体)現されている。率直な数学的表現が物理の本質を垣間見せる好例といえよう!

このとき、せん断(応)力(2コイチの偶力の片割れF(x)=F_x=F_y)を矩形型のコントロールボリュームの1辺(2次元のコントロールボリュームの場合)にそって単位長さだけ空間積分したものが(はりに曲げをもたらす)回転(応)力((応)モーメント、(応)トルク)としての曲げモーメント(2コイチの偶モーメント:応モーメント)となっている。超音波医療診断において超音波プローブを体表に押しこんだときに超音波画像(あるいは超音波画像の内部に埋め込まれた臓器やその輪郭)がたわんで見えるのも(やはり!)上記の曲げモーメント(2コイチの応モーメント)の影響によるものである。具体的にたとえば前立腺の経直腸的内視鏡超音波画像(TRUS:TransRectal UltraSound)においては、この曲げによる変形効果が患部(がん)の局在(位置とひろがり)を同定するうえでどうしても無視できなくなってきてしまうのだ(逆にいうと、深層学習による画像処理技術を援用することで臓器の輪郭をリアルタイムで精確に捉えられれば臓器内に埋め込まれた患部(がん)の局在(きょくざい)の精確な同定(どうてい)につながる)。
(参考文献)
Anju Mukasa, Norihiro Koizumi, Yu Nishiyama, Yusuke Onodera, Momoko Matsuyama, Takumi Fujibayashi, Sunao Shoji, "Development of an intraoperative cancer localization navigation system to support complete resection of prostate cancer," 36th International Congress and Exhibition on computer assisted radiology and surgery (CARS 2022), International Journal of Computer Assisted Radiology and Surgery (IJCARS), Vol.17, Suppl.1, pp.S51, 2022. https://doi.org/10.1007/s11548-022-02635-x
任意の正方行列は交代(反エルミート、歪(ひずみ、わい)対称)行列(具体的な直観的イメージとしてたとえば内(回転)力(モーメント)としてつりあいながらもコントロール・ボリュームの各面に平行なせん断ひずみ(はりの長手(ながて)方向の単位長さあたりのたわみ変形)をもたらす回転(応)力・(応)モーメント:せん断ひずみをはりの長手方向に沿(そ)って積分すればはりのたわみ(変形)をあらわす)と対称(エルミート)行列(具体的な直観的イメージとしてたとえば内力としてつりあいながらもコントロール・ボリュームの各面に垂直な垂直ひずみ(はりの長手方向の単位長さあたりの伸び変形)をもたらす並進(応)力:垂直ひずみをはりの長手方向に沿って積分すればはりの長手方向の伸び(変形)をあらわす)との和にかならず分解できるという事実もこれまた重要である。
野呂川(山形)沿いのタンポポの群生地(2025/06/05)
おのおのの(慣性・粘性・剛性:機械的パラメータに応じた)共振周波数(固有振動数)で(たわみながら)風に吹かれている!まさに自然が奏(かな)でる超偉大な( Me-DigIT ! )協奏曲(きょうそうきょく、Con Certo(カン・シェルトゥ、Von Voyage(ボン・ボヤージュ)よろしく、ここではフランス語風に乾杯っぽく発音してみよう))!
われわれの医療のデジタル化(医デジ化)研究プロジェクトで開発している医療のデジタル化(医デジ化)(超)関数(Me-δigIT generalized function)もこうありたい!と考えている。すなわち、われわれの志向するシステムの行動原理として、
『ありとあらゆる臓器のその瞬間その瞬間を切り取って(cut out)、切り取った画像や診断・術具、治療用ビームなどを適所に挿入(put in)・再配置(再構成)・合成して、臓器内(の断面)に埋め込まれた患部を抽出・摘出(cut away)・追従・診断・治療モニタリング』することができる!!!!((広義の)cut out/put in/cut away法)
(例)エミー・ネーターが研究を通じて道しるべとした行動原理は、つぎのようにまとめられるだろう。
『数や関数や演算どうしの関係性(つながり、コミュニケーション・リンク、そこで働く超偉大なるテンション(超万有引力!))を明瞭化して、統一(一貫)・統合(包括)的に適用できるようにし、その生産性を最大限に引き出すには、それを特定の対象から切り離して、普遍・一般・抽象的に有効な(メタ的な)概念として(再)表現しなおさなければならない。』
そうしてこのオブジェクト指向的な行動原理は、デジタル化ときわめて相性が良いのである!
(参考文献)
イアンスチュアート,数学の真理をつかんだ25人の天才たち,ダイヤモンド社.
産業界において現在主流の制御方式であるPID制御の基礎・基盤・土台・土俵・インフラストラクチャともなっており、工学一般において(もちろんロボット制御工学においても)極めて有用なピエール=シモン・ラプラス(Pierre-Simon Laplace, 1749年3月23日 - 1827年3月5日)が発明したラプラス変換※において微分に対応するオペレーションが代数演算的にみて、ただ単に s を関数の前にくっつけることのみになる(e-stを微分してみよ!積分は初期値を無視すれば微分の逆(演算)元となるので、単に1/sをくっつけてやれば良い)という驚くべき演算の簡便化はまさにこの効果的な応用展開の代表例である。
ちなみに、離散時間(発展)系(『離散』には値の『離散』と時間・空間・人間(じんかん)の『離散』とがある!)において(今日では一般に、デジタル・コンピュータを基礎・基盤・土台・土俵・インフラストラクチャとして用いて画像処理系および制御系を統一・統合・普遍かつメタ的に実装している。もちろんこれは、われわれのロボティック超音波医療支援システムにおいても同様である。)有用なz変換はラプラス変換のe^{-sT}をz^{-1}と置くことでむだ時間を有するシステムについて、これを巧(たく)みに表現しようとするところを起点・原点・出発点・一丁目一番地としている(もちろん、離散的に1サンプル時間だけ時間を進めるシフト・オペレータとしても有用である)。(サンプル)むだ時間分先の出力を推定・予測するうえで有用な道具立てとして代数学の父として知られるアレクサンドリアのディオファントス(推定生年 200年 - 214年、推定没年 284年 - 298年)の方程式が有名である。
ディオファントス方程式はさまざまなシステムにおいて頻回(ひんかい)に現代制御理論を援用した装備一式として具備(ぐび)され、1サンプル時刻前までの観測値を用いて環境雑音(システム雑音・観測雑音)に対して適応的に最尤(さいゆう:最小分散)推定・予測しようとするカルマンフィルタの基礎・基盤・土台・土俵・インフラストラクチャにもなっている。
1900年に提示された『ヒルベルトの23の問題』の第10問題がこの『ディオファントス方程式の一般的で有限的な可解性判定方法をもとめよ』というものであったが、これについては1970年にロシアの数学者ユーリ・マチャセビッチ(1947年3月2日-)によって否定的に解決されている。

![{\displaystyle {\mathcal {Z}}[x_{n-k}]=z^{-k}{\mathcal {Z}}[x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/889002e7427023e17c6778bb41e8b8b6f60c73db)

(参考文献)
J. Zhou, N. Koizumi, Y. Nishiyama, K. Kogiso, T. Ishikawa, K. Kobayashi,
Y. Watanabe, T. Fujibayashi, M. Yamada, M. Matsuyama, H. Tsukihara, K.
Yoshinaka, N. Matsumoto, M. Ogawa, H. Miyazaki, K. Numata, H. Nagaoka, T. Iwai,
H. Iijima: A VS ultrasound diagnostic system with kidney image evaluation
functions, International Journal of Computer Assisted Radiology and Surgery
(IJCARS) , Vol.18, pp.227-246, 2023.
https://www.youtube.com/watch?v=c7g4rfmaTd4
※ジャン・バティスト・ジョゼフ・フーリエ男爵(Jean Baptiste Joseph Fourier, Baron de、1768年3月21日 - 1830年5月16日)による熱伝導の研究を起点・原点・出発点・一丁目一番地とするフーリエ級数展開と基底関数の直交性を利用したその周波数ごとの振幅(係数)の抽出(析出:せきしゅつ)方法の発明は大きな衝撃(しょうげき)とともにその後の数学界に多くの示唆(しさ)を与えつづけた。1811年、当時43歳のフーリエ男爵は、大胆にも力強くつぎのように主張した(ときには勇気をもって大胆に主張することも(科学技術の発展においてはきわめて)重要で意義のあることである!)。
どんな関数であっても、三角関数の級数によって展開できる。級数に展開できない関数など、この世の中に存在しない!
(参考文献)
岸野正剛,今日から使える物理数学,講談社.
※※『ディオファントスの墓碑銘(ぼひめい)』として知られる問題がある。
{\displaystyle {\begin{aligned}a_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }f\left(t\right)\cos nt\,dt,\left(n=0,1,2,3,\dots \right)\\b_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }f\left(t\right)\sin nt\,dt,\left(n=1,2,3,\dots \right)\end{aligned}}}
指数関数のようなよく知られた初等関数であっても、指数部に虚数(や後述するラプラス変換のように複素数)を(ただ!)持ち込むことでまったくあらたな性質を帯びてくる(世界が違って見えてくる!)というのである!具体的にフーリエ級数は複素フーリエ級数へとその姿・形を柔軟に変化・変容(transform)・洗練(sophisticate)・進化(evolve)させてゆく。これにともない、(円分体(えんぶんたい)をその基底とする、N→∞次元の多角形の)レーダーチャート(Radar Chart)のような世界観が顕在化(けんざいか)する!
具体的にまずはこの正弦・余弦から複素フーリエ級数への移行にともなってフーリエ級数c_nは複素数化される。この複素数c_nは、(基底関数ベクトルである)e^{inx}と掛け合わされ、さらには有名なオイラーの公式を用いてcos波(実部)とsin波(虚部)の合成波の形で表現されることから波動の振幅および位相という2つの(複数の!)情報を包含(ほうがん)しうることが示される(率直な数学的表現が物理の本質を垣間見せる好例といえよう!)。現在工学で用いられている表現形態はその直観的な見通しの良さ、扱いやすさから、十中八九この複素数表現になっている。
つぎにクロネッカーのデルタ関数の添え字のi,jを連続化してディラックのデルタ関数δ(i-j)を創ったように、c_nの添え字(n)の(時間領域あるいは空間領域における)連続化、すなわち(連続的な数である実数の)周波数(ξ=n/T:クシー)を導入することによる(複素)フーリエ級数の連続化が図られた。
ここで、c_nの値はもともとの関数f(t)と(基底関数ベクトルである)e^{int}との内積(正確には内積の複素解析版であるエルミート積、したがって積分の中身はf(t)とe^{int}の複素共役であるe^{-int}との積になっていることに注意されたい)をとることによって簡便に求めることができ、積分区間の長さ2π(円軌道の周長は2πrであることに着目されたい)で割ることによって周波(振動)数ごとに(円)振動の動径(振幅)を得ている。
また、複素フーリエ級数のΣの中身であるc_nとe^{inx}の積は(円分体(えんぶんたい)をその基底とする)レーダーチャート(Radar chart)よろしく!複素数の極座標表現の形になっていることにも着目されたい。すなわちこれは、固有値(動径:どうけい)である1次元エルミート行列(c_n)と(蛍(ほたる)の光※よろしく!周期的な(円)振動を表現する)固有関数ベクトルである1次元ユニタリ行列(e_{inx})の積による固有(円)振動を表現しているのだと捉える世界観もこれまた重要である(率直な数学的表現が物理の本質を垣間見せる好例と言えよう)。Con Certo(カン・シェルトゥ、Von Voyage(ボン・ボヤージュ)よろしく、ここではフランス語風に乾杯っぽく発音してみよう)!
※蛍の光の明滅を見ると、心が和(なご)む。 蛍の腹部(ふくぶ)から発せられる淡い光の明滅は 正弦波(あるいは余弦波)をLEDに与えることによって(デジタルに!)再現できる。呼吸で取り入れた酸素が発光器の中のルシフェリンとルシフェラーゼに届くと光が出て、酸素の供給が遮断されると光が消える。この酸素供給のオン/オフは脳からの神経シグナルで制御されており、複数の蛍が当初はバラバラの点滅をしていたとしても、しばらくすると周囲の蛍の明滅と同期する。すなわち群として、
あたかもオーケストラの協奏曲(Con Certo(カン・シェルトゥ、Von Voyage(ボン・ボヤージュ)よろしく、ここではフランス語風に乾杯っぽく発音してみよう))を奏(かな)でるように呼吸のリズムを統合・調和(harmonize)させている!
西日本型ゲンジボタルは、同期明滅時の発光間隔が2秒(0.5Hz)と言われている。
(参考文献)
{\displaystyle \sum _{n=-\infty }^{\infty }c_{n}e^{inx}=\lim _{m\to +\infty }\sum _{n=-m}^{m}c_{n}e^{inx}}
さらにその後、特定の周期をもたない関数をも包含した一般の[-∞, +∞]区間の関数に対してもフーリエ級数の世界観の及ぶ範囲を適用拡大しよう!とする試みがなされ、フーリエ級数はフーリエ変換へと進化した。これに応じてフーリエ級数における(離散的な)(振動)周波数の『和(sum)』はフーリエ変換においては連続的な(振動)周波数(ξ=n/Tあるいはξ=n/L)による積分表示の形式へと進化している(フーリエの積分表示)。
具体的に時間領域(t)あるいは空間領域(x)の関数を(振動)周波数領域(ξ=n/Tあるいはξ=n/L)の関数へと変換する(複素)フーリエ変換、およびその逆変換である逆(複素)フーリエ変換の発明がなされ、さらには超関数(ちょうかんすう)の概念をも用いて苦心してその微分・積分演算が発散することなくできうるかぎり何らかの値をもつように工夫したメタ(包括)的な拡張概念としてのラプラス変換およびその逆変換であるラプラス逆変換へと発展してゆく。
古典制御理論の基礎・基盤・土台・土俵・インフラストラクチャともなっているラプラス変換およびその逆変換であるラプラス逆変換では上記の2πiξ(=jω:ここでiもjもおなじく(純)虚数をあらわすことに注意されたい。電気系では電流のiとの混同をさけたいがために、電流のiを優先して複素数のiのほうをあらためてjで置きなおすことが常態(じょうたい)・慣習化している。)をあらためて(複素数)s(=σ+jω)と形式的に置きなおす。
すなわち実数の角(振動)周波数ω(=2πξ)からs(=σ+jω)へと、さらに複素角(振動)周波数化※することによって過渡的な信号(応答)波形の一般的な表現(形式)をもその内部に組み込んだことが本質・本格的な進化へとつながった。
※すなわち、実数xを複素数z=x+iyへと拡張することによる実関数の複素関数化としての複素指数関数、複素三角関数の導入・実装である。
具体的にjω(純虚数)に代えてσ+jω(=s:『実数部と虚数部』を合わせもつ複素数)という変数(複素角(円)(振動)周波数)をあらたに導入・実装することによりわれわれは最終的に、定常的な応答(振幅が一定で変わらない正弦波および余弦波(波形))のみならず過渡(経時)的な応答(時間とともに減衰あるいは発散する正弦波および余弦波(波形)あるいはこれらを合成した減衰あるいは発散する円振動)の表現方法をも装備一式としてその手中におさめ、これを巧みに制御・ハンドリングすることができるようになったのだ。
ここで、(複素)フーリエ変換およびラプラス変換表現はオイラーの恒等式の援用(えんよう)により、複素角(振動)周波数(スペクトラム)の振幅のみならず位相の表現をも損なうことなくうまく包含(ほうがん)できていることに着目されたい。このことが、ありがたくも(複素)フーリエ変換およびラプラス変換とそれらの逆変換との間の可逆(かぎゃく)性を巧妙に担保(たんぽ)してくれているのである。
また、(複素)フーリエ変換およびラプラス変換表現は積分の中身が(関数ベクトルの一致度を評価する)内積の複素解析版であるエルミート積になっていることにも留意されたい(したがって基底関数ベクトルe^{2πixξ}およびe^{st}の複素共役e^{-2πixξ}およびe^{-st}が用いられている)。
内積の演算は(関数)ベクトルのノルム(大きさ)や相関(一致度)を計算するために頻回(ひんかい)に用いられる装備一式であるが、ここでは、周波数領域(ξやs)のスペクトラム波形(フーリエ変換やラプラス変換そのもの)から時間(t)あるいは空間(x)領域の波形を復元・(再)構成するために用いられている。
(参考文献)
フーリエ級数がもたらした『無限級数(関数の基底)により一般的な関数が分解、復元、再構成・再構築(再表現)されうる』というあらたなるものの見方・考え方・捉え方・発想の仕方・世界観は、集合論の基礎を築いたゲオルグ・カントールによる実無限(じつむげん)の概念との間にも重要なコミュニケーション・リンク(およびそこで働く超偉大なるテンション(超万有引力!))を有しており、数学のみならず、さまざまな分野においてその世界観にきわめて重大な影響を与えた。
(参考文献)
現代数学を生み出した無限集合
また、無限級数(関数の基底)(系)の構成要素であるひとつひとつの直交関数をあらたに基底(関数ベクトル)として捉えなおすことで、計量線形性を有するユークリッド空間の概念を普遍・一般・抽象化したメタ的な概念である一般の可算(無限)次元ヒルベルト空間※※の概念へと発展した。
ここで、『関数を無限次元のベクトル(や行列(写像))である※』と普遍・一般・抽象化して、メタ的な概念として捉える世界観、換言(かんげん)すれば『ベクトル(や行列(写像))は関数概念の一般化である』というメタ的な認識こそが数学(物理学、工学一般、もちろん医療解析やわれわれの人工知能援用医療ロボット工学においても!)の発展の歴史のなかできわめて重要な役割を果たしてきたことに気づく。ここで行列(写像)を、ベクトルに次元を追加したもの(ベクトルの一種)だと認識・解釈することができる(世界観!がある)ことに留意(りゅうい)されたい。すなわち、『行列』は文脈に応じて臨機応変に第1義的には『ベクトル』と捉えてもよいし、もちろん、これに次元を追加実装することで第2義的には『行列』と捉えてもよい!のである。
『関数とは一つの解析的な式である』という18世紀風の世界観から離れて(Off to see the world !)物体の(自律的な)運動軌道など、何らかの関数値を[f(x_0), …, f(x_n)]と(有限個あるいは可算無限個の点によって有限個あるいは可算無限個の区間に分割し)順々に並べてみれば、たしかにベクトル空間(あるいは次元をさらに追加実装した行列(写像))としての分解・再構築(再表現)が可能であり※、関数における特異点は(地形的にみれば)その近傍の(崖(がけ)から一気呵成(いっきかせい、カスケードに)に流れ落ちる瀧(たき)が如(ごと)き)無限大に発散する急勾配(差分)を特徴量として(上記の)ベクトル空間(あるいは次元をさらに追加実装した行列(写像))に埋め込まれることであろう(ここで、(ベクトル)空間を点の集合であると捉える世界観が重要である!ことを今一度思い起こしておこう。すなわち連続的な関数は(有限個あるいは可算無限個の点で構成される)ベクトル空間(あるいは次元をさらに追加実装した行列(写像)を被覆(ひふく)するという意味において非可算無限個の点からなる『被覆空間』となっているのである)。
※ある区間上の連続関数全体の空間は(可算あるいは非可算)無限次元と捉えることができる。実際,単項式関数1, x, x^2,‥は線形(1次)独立であり、これらの基底の線形結合で表現できれば、その関数は可算無限次元(のベクトル空間である)と捉えることができる。あるいは数直線上の点x=aにおいてのみ1となり、x≠aでは0であるディラックのデルタ抽出関数δ(x-a)を基底として用いれば連続(非可算)無限次元(のベクトル空間である)と捉えることもできよう。バナッハやヒルベルトが志向したのは、究極的にはこのような(自由で、なおかつ自在な空間の)捉え方(世界観)であろう。
一見したところ、なにも関係がないように思われる関数とベクトル(あるいは行列(写像))との間には、実に驚くべきことだが、関数のベクトル(あるいは次元をさらに追加した行列(写像))表現にもとづくきわめて偉大なコミュニケーション・リンク(およびそこで働く超偉大なテンション(超万有引力!))が存在していたというわけある。
※試しにベクトルの要素をひとつのタイルに書き込んで、これを面状(2次元的)に敷き詰めてみれば行列(写像)としての分解・再構築(再表現)が可能であるし※※、その逆もまた可能で、面に対して敷き詰められた(たとえば超音波画像における輝度値などが書かれた)タイルを引っぱがしてきて、これを線状(1次元的)に並べ直してみればベクトルとしての分解・復元・再構築(再表現)が可能であることに留意(りゅうい)されたい。画像をベクトルとみるべきか、あるいはこれに次元をさらに追加して行列(写像)とみるべきかはわれわれの解釈・認識(世界観)の問題であり、TPOに応じて都合よく使い分ければそれでよいのである。
(参考文献)
ラプラス変換において畳(たた)み込み積分という概念が出てくるが、英語ではConvolutionalで直訳すれば『(ぐるぐると!)巻き込みながら畳み込んで行く』という意味である。この積分はプリンタで(ぐるぐると!)巻き込みながら(各色を)畳み込んで転写(てんしゃ)するというのが直観・幾何学・野性的に見通しの良いイメージで、右手(系)と左手(系)、カギとカギ穴、ハンコと印影(いんえい)のように反転ずらし(ひっくりかえして鏡像をつくってずらす)で(内積によってベクトルの相関・一致度、すなわち)重なりを見る演算であることを数式の構成が率直に表現している(率直な数学的表現が物理の本質を垣間見せる!)。
畳み込み積分はロボット工学をはじめ、システム制御の分野でも有用かつ頻回(ひんかい)に用いられており、その積分の中身は『インパルス入力(f(t)dt)と(風が吹けば桶屋が儲かる式の連想・伝言ゲームよろしく!時空人間を隔てるごとにその相互関連(そうごかんれん)性(重みや勾配)が減衰しながら(あるいは伝言ゲームにおいては尾ひれはひれなどもともなって当初の伝言内容が)薄まってゆくような(残存)影響力の相互)伝達関数(伝言ゲームにおける伝言内容の伝達効率や一致度)g(t_0-t)との掛け算(内積)』として捉えることができる。
さらに可制御正準系と呼ばれる
状態空間表現(現代制御理論)と伝達関数表現(古典制御理論)との間の相互の結び目(TIE、絆、超万有引力)についてより深く学べば、その応用展開に関する直観・幾何学・野性的に見通しの良いイメージや深い考(洞)察が得られるであろう(すなわち、時・場所・人を隔てると一般にその事象の影響力は徐々に薄まってゆくのだ!だからこそ、時空人間を超越した超万有引力の存在はありがたいのである!とも言える)。またこの畳み込み積分の概念を(風が吹けば桶(おけ)屋が儲かる式の連想・伝言ゲームよろしく!)普遍・一般・抽象化してメタ的に捉えれば、われわれの脳のモデルたる畳み込みニューラルネットワークの概念にも発展的につながっていることに気づけるであろう。
すなわち、
人生を(余すところなく謳歌(おうか)、)全(まっと)うするためには自身の人生における伝達関数の極、系の固有方程式の根より生まれ、そして成長するためのしっかり・くっきり・はっきりとした強固な軸(じく)や芯(しん)たる超固有モード(超固有値・超固有ベクトル)が要求され(、その成長はドラゴンボールに出てくる、『精神と時の部屋(Me-DigIT ! AI-enhanced Robotics Researching Room of Spirit and Time)』よろしく!人工知能・IoT・ロボット技術の援用により、(その極限にむけてみずから)さらに加速・進展しう)る!
(参考文献)
小郷 寛,美多 勉,システム制御理論入門,実教出版,1980.
人間のDNAもこの手法によって(ぐるぐる巻きに!)転写(てんしゃ)・複製されており、風邪を引いたり、ワクチンなどで獲得した免疫抗体(めんえきこうたい)が侵入物であるウイルス(抗原:こうげん)をキャッチすることができるのもこのカギとカギ穴を用いた原始的だがきわめて強力な方法のおかげである。
わざわざ、複素共役(ふくそきょうやく)なる(双対:そうつい/そうたいとなる)数をつくって掛(か)け合わせて(エルミート積と呼ばれる内積の複素拡張である!)ノルム(距離や大きさ)を計算したり、行列やベクトルを転置(天地!ひっくり返)して、さらには複素共役までとって(双対となる)随伴(ずいはん)行列※なるものをつくって対応する行と列を掛け合わせて内積をとって、あらたな行列の成分要素とするのも偏(ひとえ)にこの反転ずらし(ひっくりかえして鏡像※をつくってずらす)で(内積によってベクトルの相関・一致度、すなわち)重なりを見る演算をしたいがためである!
※鏡像によって負の長さ、面積、体積なども定義することができる。
鏡像(ひっくり返し、Mirror Image)にもヴァラエティ(Variety)があって、単位円(反転円、一般化して超球面)に対する鏡像(ひっくり返し、反転、円(一般化して超球面)に対する鏡像・反転)、実軸(直線、一般化して超平面)に対する鏡像(ひっくり返し、反転、直線(一般化して超平面)に対する鏡像・折り返し)など、いろいろさまざまある。
実軸方向の反転(ずらし)が畳み込み積(和)分、虚軸方向の反転がエルミート積(和)分であり、いずれも対応するベクトル成分を掛け合わせて(ぐるぐる巻きに畳み込みながら!)足しこむという相関一致度を評価するための内積(和)分演算手法を鏡映(きょうえい)あるいは並進対称性へと適応拡大して直観・幾何学・野性的にも見通し良いものにしようとする亜種(あしゅ)的手法としてこれらを統一・統合・普遍的に抽象化してメタ的に捉えることも可能である(自身の姿かたちを評価するために鏡(姿見、Mirror Image)を用いるのは直観的にもきわめて有効な手段であろう!)。
※ここで、重なりが完全一致したときの内積の値は、そのベクトル自身の大きさ(ノルム)の平方(2乗、自乗)になっていることに留意されたい(このノルム(norm)によって規格化(normalize)された値がベクトルのなす角の余弦(cosθ)となっており、相関係数とも呼ばれる!相関係数は2つの変数の間にどの程度、直線的な(1次の)関係があるかの指標(index)となっている。
古今東西、世の中の問題を解くためのカギの多くは(なんと!)この『反転ずらし』という古典的で簡便だが強力な(そうしてきわめて人間くさい!?(レーザプリンタの感光ドラムよろしく!)ぐるぐる巻きに畳み(足し)込んでゆく)手法を基礎・基盤・土台・土俵・インフラストラクチャにして創(つく)られていたというわけである!『幽霊(ゆうれい)の正体(しょうたい)見たり!!!!』である!
※Gを群、HをGの部分群(同値類の集合)とするとGの(Hによる)同値関係~は以下で定められる。ここにもやはりというべきか、『反転』したかけ算(内積)の型(かた)が現われる!
近年発展の著しい畳み込みニューラルネットワークも基本的には同じ手法(やり口)で輪郭形状や模様(テクスチャ)といったパターンの相関・一致度を見ている。具体的には入力画像と学習した勾配画像特徴量ベクトルとを反転ずらしで(ぐるぐる巻きに)重ね合わせて足しこむ内積(ドット積)の演算により相関一致度を見ているのである。
これを画像を折りたたみながらマルチスケールかつ多(深)層で行なうことで大域的あるいは局所的なパターンをきわめて簡便かつ高精度に抽出・追従・モニタリングすることができ、ロボットビジョンやわれわれの医用画像処理の分野においても頻回(ひんかい)に用いられるようになってきている。
具体的に例えば臓器内に埋め込まれたがんや結石をはじめとする病変の位置と広がり、すなわち局在(きょくざい)を非常に精度よく同定(どうてい:一意にさだめるということ)して局所的にピンポイントで治療したり、ロボティック超音波診断において診断画像の適正度を評価したりするのに役立つ、きわめて優秀な抽出関数が出来上がる(われわれはこれをMe-DigIT Harvest 抽出関数と呼ぼう!)。
上記でいくつか例をみたようにフーリエ級数がもたらした『無限級数(関数の基底)により一般的な関数が再構成・再構築(再表現)されうる』というあらたなるものの見方・考え方・捉え方・発想の仕方・世界観は工学的解析(もちろん、医療解析やわれわれの人工知能援用医療ロボット工学)においてもきわめて重要な世界観となっている。具体的にたとえば、
われわれの医療のデジタル化(医デジ化)研究プロジェクトとは、専門家の医療技能を機能(関数)として捉えて、その基底となる関数を抽出・分解・再構築(再構成、構造化)して、医療支援システムの機構・制御・画像処理・アルゴリズム上にひとつひとつデジタル機能関数(Me-δigIT function)としてAI・ロボティックに実装しよう
とするものである。これにより、医療の質や生産性の向上が極限まで高まるものと強く期待されている。
(例)エミー・ネーターが研究を通じて道しるべとした行動原理は、つぎのようにまとめられるだろう。
『数や関数や演算どうしの関係性(つながり、コミュニケーション・リンク、そこで働く超偉大なるテンション(超万有引力!))を明瞭化して、統一(一貫)・統合(包括)的に適用できるようにし、その生産性を最大限に引き出すには、それを特定の対象から切り離して、普遍・一般・抽象的に有効な(メタ的な)概念として(再)表現しなおさなければならない。』
そうしてこのオブジェクト指向的な行動原理は、デジタル化ときわめて相性が良いのである!
(参考文献)
イアンスチュアート,数学の真理をつかんだ25人の天才たち,ダイヤモンド社.
※※ヒルベルト空間は内積(ないせき)の演算を装備一式として具備(ぐび)した、計量線形(関数ベクトル)空間であるが、そこから計量(すなわち基底の直交)性の条件のみをあえて外(はず)して(ゆるめて)普遍・一般・抽象化してメタ的に捉えなおした、定数倍の足し算(すなわち1次線形性)までを演算規則として具備(ぐび)する、バナッハ空間という(1次)線形(関数ベクトル)空間の概念もある。
ヒルベルト空間(基底が直交している内積空間の一般化)もバナッハ空間(かならずしも基底が直交していることを要求しない射影空間の一般化)も歴史的にみてフーリエ級数をその起点・原点・出発点・一丁目一番地・スターティング・ポイントとしており、可算(さらには連続)無限次元の関数空間を強く意識した概念として生まれてきたという経緯(けいい)がある。
バナッハ空間は『中身のぎっしり詰まった』完備(かんび:コーシー列a_nが収束する)な実数(1次線形性を有する空間であるが直交性の概念まではこの段階ではまだ要求していないことに留意されたい(したがって、直交していなくても良いし、もちろん直交していても良い。すなわち、ヒルベルト空間から直交性の条件のみをゆるめて捉えているということである!))を普遍・一般・抽象化して一般の可算無限次元へと拡張したメタ的な概念として捉えることもできる(ラーメンと麺類の関係よろしく、ときにはあえてある条件のみをゆるめてみる(機械装置の構造部材を組みあげるためについているねじをドライバーでゆるめてみるようなイメージ、実際にゆるめずとも仮想的に頭の中でねじをゆるめて思考実験するだけでも十分に有効!)ことにして(実装)解空間を拡げてあらためて(『
洛中洛外図屏風(らくちゅうらくがいずびょうぶ)』)よろしく!より高みから俯瞰(ふかん)して)見直してみること(
Off to see the world !)も(戦略的に!)きわめて有効な方法だ!)。
(実装)解空間やその拡大の方法を考えるにあたっては、方程式が代数的に解ける条件に関するエヴァリスト・ガロア(ガロアは1832年、決闘による傷がもとで20歳のきわめて短い生涯(しょうがい)を終(お)えた)の理論やこれにともなう体の拡大、像空間(ぞうくうかん)が縮退(しゅくたい)すれば解空間が拡がることを率直に表現している線形代数学の基本定理等について深く学ぶ必要がある。ガロアはまず、『ガロア群が(可解(かかい)群という言葉によって一言でまとめられる)ある性質をもつ群であれば、その方程式が代数的に解ける』ことを示した。
つぎに、上記の逆命題(めいだい)である『方程式が代数的に解けるならば、ガロア群が可解群の性質をもつ』ことを示した。この対偶(たいぐう)命題をみることによって、『ガロア群が可解群の性質をもたないならば、方程式が(一般には!ひとくくりに)代数的に解けない』ことがわかる。最後に、ガロア群が可解群の性質をもたないことを示すことによって、一般の5次方程式が代数的に解けない(もちろん条件しだいでは例外的に解ける場合もある!)ことを証明した。
(参考文献)中村亨,ガロアの理論,講談社.
ヒルベルト空間もバナッハ空間も一応は、可算無限次元までを対象とした概念ではあるものの有理数からの実数の析出(せきしゅつ)よろしく、離散的な基底パラメータ表現を連続的な基底パラメータ表現に置き換えたフーリエ積分公式などを観てみれば、本質的にはさらに連続無限次元空間へのさらなる拡張を指向(しこう)しているとも言えよう。
その空間のなかで任意のコーシー列が収束するような空間を『中身のぎっしり詰まった』完備(かんび)な空間という。『中身がぎっしり詰まって』さえいれば、大河のひと雫(しずく)、サハラ砂漠の砂粒(すなつぶ)よろしく、(イデア論的には!)極限としての解の存在が(かならず!)保証されるため、そこでは微分積分学の装備一式が有効に機能する。
ここで内積による計量(すなわち基底の直交)性の条件を外した一般の(1次)線形(関数ベクトル)空間であっても、寄り道をすれば長くなる性質(三角不等式)など、距離(ノルム、長さ)の概念を導入・実装した距離空間が構成できることに着目されたい。
距離(ノルム、長さ)の概念が導入・実装できればロボットによるフィードバック追従制御を実装することは十分に可能である。すなわち、ロボティック超音波診断・治療支援システムにおいて臓器内に埋め込まれた患部(がんや結石等)をロボティックに抽出・追従・モニタリングするうえで、かならずしも視覚センサである超音波プローブが直交していることまでは(じつはまだ)条件として要求されていないことがわかる(もちろん直交していれば直観・幾何学・野性的に見通しが良くなるため、それに越したことはない)。
これについてより詳細を知るためには、(1次)線形代数学における縮小写像(しゅくしょうしゃぞう)の原理について学ぶ必要がある(このとき臓器内に埋め込まれた患部は超音波画像上において不動(ふどう)点として蝶(ちょう)の標本(ひょうほん)のごとくピンフォール(抑え込み、ピン止め)固定される)。
静中動(せいちゅうどう)あり、動中静(どうちゅうせい)あり
超音波診断装置で画像を時間軸上の一点でピン止め固定するボタンをフリーズ・ボタンと呼ぶが、空間上の一点を不動点として超音波画像をピン止め固定するためには上記のフィードバック追従制御の実装が必要になる。プロレス技のピンフォール(抑え込み)よろしくターゲットが時間軸あるいは空間上でピン止め固定された世界では、医療診断や治療がきわめて容易なものとなる。
(複数の(マルチな)世界観を巧(たく)みに活用する法)複数の(マルチな)世界観をいい所取りしながら融合的に用いて(場合によっては巧みに使い分けながら)解析を進めてゆくのは戦略的にすぐれたうまいやり方である。具体的に医用画像においては、X線CT、MRI、SPECT-CT、超音波画像など複数の医用画像診断モダリティ(modality)が存在し、それぞれにはかならず得手・不得手が存在する。これらの得手・不得手を考慮して融合的に用いることで、病巣の局在を高精度かつ頑健(ロバスト)に同定することができよう。
(参考文献)
Anju Mukasa, Norihiro Koizumi, Yu Nishiyama, Yusuke Onodera, Momoko Matsuyama, Takumi Fujibayashi, Sunao Shoji, "Development of an intraoperative cancer localization navigation system to support complete resection of prostate cancer," 36th International Congress and Exhibition on computer assisted radiology and surgery (CARS 2022), International Journal of Computer Assisted Radiology and Surgery (IJCARS), Vol.17, Suppl.1, pp.S51, 2022. https://doi.org/10.1007/s11548-022-02635-x
Daiki Inaba, Norihiro Koizumi, Yu Nishiyama, Kunishima Atsushi, Yoshiki Ikeda: Artificial Intelligence Assisted Preoperative Diagnosis Support System for Ovarian Tumors, 38th International Congress and Exhibition on computer assisted radiology and surgery (CARS 2024), International Journal of Computer Assisted Radiology and Surgery (IJCARS) , Vol.19, Suppl.1, pp.S146-S147, 2024. https://doi.org/10.1007/s11548-024-03128-9
また、同じ極座標を用いるにしても、まずは実平面と複素(オイラー)平面をまずは同時に設定してみて、両者の得手・不得手を考慮しながら(両にらみで)巧みに解析をすすめてゆくのも複眼視(マルチセンシング)によるきわめて有効な戦略である。なぜなら抽象化の階段を一段登って(条件(ネジ!?)をゆるめて)普遍・一般・抽象化してメタ的に考えてみれば、これら複数の(マルチな)世界観は上層においてはひとつながりになっており、同じモノの表裏(異なる側面)を表現しているにすぎない場合がきわめて多いからだ。
(知性・知能との超偉大なるコミュニケーション・リンク生成による野性・野能の変化・変容・洗練・進化法)~~~~~~~
『(衝動的に!)やらずにはおられないこと』はわれわれ人間が一個の動物の精神機構として個人個人に対して固有に与えられた天賦・天性の『野性・野能』が本質・本能的に求めるもの、いわば『天からの贈り物(a gift from heaven)』である。
われわれはこのかけがえのない天賦・天性の能力である『野性・野能』という『天からの贈り物』を『知性・知能』によって柔軟(topological)に変化・変容(transform)・洗練(sophisticate)・進化(evolve)させるべきである。換言(かんげん)すれば、『知性・知能』を『野性・野能』に従わせるべきであるという立場をとることにする。なぜなら、
せっかくわれわれ個々の動物(ここで、人間∈動物であることに着目されたい)に与えられた(ひとりひとりに固有の人生を全(まっと)うするための固有値・固有(関数)ベクトル(空間)を産み出すエネルギーの源泉、エンジンたる原動(能)力(属性)である!)天賦・天性の『野性・野能』という輝かしい能力(軸)を、『知性・知能』によって過度に抑制(圧)してしまったり、失ってしまったりするということは自然の摂理(providence of nature)に反しているし、まず何よりもこれ(独自の精神機構にもとづく『野性・野能』という輝かしい能力)をうまく活かしきれずにいることは生命の神髄(クイントエッセンス)を無視した、とても勿体(もったい)ないことではないか!?と考えるからである。
(例) 夢・野心・野望・欲望というものは個人個人異なる天賦・天性の『野性・野能』(もちろんこれは、『知性・知能によって変化・変容・洗練・進化した『野性・野能』であっても良い)という輝かしい能力(軸)がその時々におかれた環境(一は全、全は一よろしくわれわれ人間もまた、その環境の一部※である!)との邂逅(かいこう:出会いのこと)によって生じた超偉大なるコミュニケーション・リンク(およびそこで働く超偉大なるテンション(超万有引力!))に応じて相互モーメントや時には(バチバチと)化学融合反応を伴ないながら産み出されるべきものであり、個人個人異なる人生の(最終)目的(地)となりうるべきものである。
※人は満員電車に不平・不満を言いがちだが、自分自身も満員電車(という環境)の構成要素になっている(一は全、全は一である!)ことを忘れがちである。良質の環境(データ)が良質の運動知能をつくる(もたらす)!
人工知能によってたとえその分解・再構築・再表現が可能であったとしても、ひとりひとり異なる多種多様、さまざまな夢・野心・野望・欲望(これらはわれわれ個々に人生を全(まっと)うするための固有(関数)ベクトル(空間)をもたらす)をその個人と全く同様の熱量(人生を全うするための固有(関数)ベクトル(空間)に対応する人生を全うするための固有値、すなわち独自の固有モード(自分軸)※)をもって、同様に描き続けることは困難であろう。
すなわち、ある個人がおもしろいと思ったことを(そのままでは)赤の他人である人工知能が赤の他人である我々のために自発的に独自の固有モード(自分軸)にもとづく問いを発しつづけながらこれを解決すべく、とことんまで、どんどんやろう!などとはけっして思わないだろう。
なぜならその個人を中心として世界を観るとき、その個人と全く同じ天賦・天性の『野性・野能』をもつわけではない人工知能にはモチベーションの初期(パラメータ)値としてそう(設定)するべき必然性(ひつぜんせい)が全く存在しないからである(モチベーションの固有値・固有(関数)ベクトル(独自の固有モード(自分軸))を天から与えられるべきはいつも個人個人である!)。他方で人工知能は独自の固有モード(自分軸)をもつ人・事業にとってはこれを掛け算によって多元的にブーストしてゆく大きな力を与えてくれる。
※一般に(1次)線形代数ではある固有値に対応する固有(関数)ベクトル(空間)という表現が頻回(ひんかい)に用いられる。これは線形代数の固有値問題を解く手順が、特性方程式を起点として、まずはその(特性)根を求めて固有値たりうるかどうかを判断する。つぎに、これに対応する固有(関数)ベクトル(空間)を同定するというステップを踏むためである。異なる固有値に対しては異なる固有(関数)ベクトル(空間)が対応する。
他方、われわれの時系列的な感覚としては固有値よりも固有(関数)ベクトル(空間)のほうが先行しており、より根源的なモノと捉えているように思われる(感ぜられる)。固有(関数)ベクトル(空間)がまずは生じてつぎに、これに対応する固有値が果たしてどれだけ宿り、付随(ふずい)して生じてくるだろうか?と考えるほうが我々にとってより本質的かつ自然な思考の順序に思われる(感ぜられる)からである。
(例)現代数学の教科書においてはまず『行列』が登場し、つぎに『行列式』が登場するが、歴史的には『行列』よりも『行列式』のほうが先に登場した。日本が世界に誇る和算家である関孝和(1642-1708、せきたかかず)が行列式を生み出したのは、『2つの方程式が同じ解をもつかどうかを判定する式』である『終結式(しゅうけつしき)』をハンドリングしたいがためであった(シルヴェスタの終結式とも呼ばれる)。終結式=0の場合には、2つの方程式が共通の解(零点)をもつことになる。
(参考)
竹内淳,高校数学でわかる線形代数,講談社.
(例)自分のどうしてもやりたいこと(固有(関数)ベクトル)がまずは生じて、つぎにこのために必要な固有値(熱意・人・モノ・カネ・研究プロジェクト・研究室・企業などのコンビネーション)の工面(くめん)の必要性が(必然的に!)付随(ふずい)してくる。すなわち、『あんなこといいな♪』と考えるのび太君とそれをなんとか一般化n次元ポケット(時間・空間・人間のなかのコンビネーション)から道具を工面して実現しようとするドラえもんとの関係である。
固有値と固有(関数)ベクトルをひとまとめにして、固有モードと呼ぶこともある。固有モードは機械系においてシステムの固有振動数(電気系においては固有周波数)を扱う際などに頻回(ひんかい)に利用されている重要な概念であり、医療ロボティクス分野においても治療用超音波(HIFU)の発生や、ロボットの安全・安心・安定的で( Me-DigIT 魂のこもった!)思いやりのある制御においてもこれまた、とてつもなく重要な概念である。
固有(関数)ベクトル空間を拡張した概念として一般化固有(関数)ベクトル空間(T不変部分空間)と呼ばれるものがある。オペレーション(T)が何度加わっても、固有(関数)ベクトルおよび固有(関数)ベクトルをもとに拡張された一般化固有(関数)ベクトル空間の基底の線形(1次)結合はしぶとくその空間の住民でありつづける。
心のなかにけっして折れることのない一本の槍(人生を全うするための固有(関数)ベクトル空間)を宿した人間はその空間の住民として、とにかく『しぶとくて一途(な愛すべき引きこもり、数学の言葉でいうところの群やイデアル※・体)』なのだ。空間どうしが一般化固有(関数)ベクトル空間(T不変部分空間)でお互いに引きこもってしまい、原点を除けば互いに交わりがない関係にある場合、それらの空間は互いに直交補空間の関係にあるという。
※『加法』(和)および『乗法』(積)と呼ばれる二種類の技(演算)を備えた土俵(したがって、加・減・乗までの演算が実装され、その動作が保証された代数系)である環(Ring)Rの部分環Iをイデアルとよぶ。すなわち、マトリョーシカ(構造)よろしく、土俵(上の技の集合)の部分(集合)が、これまたひとつの土俵(上の技の集合)になっている(という再帰的な入れ子構造である)。再帰的ではないが、ユークリッド運動群のなかに、並進運動群と回転運動群とが埋め込まれている(入れ子構造となっている)こととSimilar (analogous, 類似)である。『イデアル』という呼び名はクンマーがフェルマーの最終定理の証明を試みた際に名付けた『理想数(ある環の中の『いい感じの部分集合』といったくらいの意味合いである!)』という(数学的)概念が元ネタであるという。
(参考)じっくりガロア理論解説13-イデアルと商環
I⊂R(イデアルは環の『いい感じの部分集合』である!)
(まずは)好きなことをしよう(固有(関数)ベクトル(空間、群・イデアル・体、土俵(上の技の集合)・住み処・宿り木)を見定めよ!)。
(つぎに)していることを愛そう(固有値を高めよ!)。
ピーター・フレミング
Find and do what you love (at first), (next) love what you do.
Peter Fleming
君の魂の中にある(生命の神髄(クイントエッセンス)にもとづく)英雄(人生の固有(関数)ベクトル空間、群・イデアル・体、土俵(上の技の集合)たるHeroの道)を放棄(abandon)してはならぬ。
どんな状況であれ(Under no circumstances)、
自分を卑下(despise)することなかれ。 気高くあれ(Be noble、人生を全うするための固有値を高めよ)。
我々の心に宿す神性(divinity)は、 (人生を全うするための固有(関数)ベクトル空間が)絶える(縮退する)ことのない不滅の存在(constant & immortal being)である(ことを我々自身に要求する)。
魂の中にある神(の道)を見定めよ(Determine the god in your soul)。
(Friedrich Wilhelm Nietzsche)
たった一度でいい。本当に(MeDigIT!)魂が震えるほどの悦び(人生レベルでの感動体験、共振現象!)を(何かに対して)味わってしまったのなら、その人生は生きるに値する。悲しみ、苦しみを引き連れて『よし、もう一度この(MeDigIT!)人生を』と言いうるだろう。
(Friedrich Wilhelm Nietzsche)
Hero (Mariah Carey)
他人の意見(を自分軸で評価することもせずにただ単に鵜呑(うの)みにすること)で(生命の神髄(クイントエッセンス)にもとづく)自分のほんとうの心の声(自分軸)をかき消してはならない(Steve Jobs)
君はただ、自分(の固有軸)を肯定すればいい
(Nietzsche)
他人(軸で)の評価が気になってしまうことで自分自身が本来やりたかったことが何もできないでいることがある(そうしてこのような状況はとてもとてももったいない状況ではないか!そうして個人個人の幸福への道にもつながりにくいように思われる)。そういう場合には、私には腹にくくった(決意の一本)槍(やり)として命をかけられる○○(人生を全うするための大切な固有(関数)ベクトル空間)があり、(慣性力をそのままに)そこを突き進められているのならば(その瞬間において)人にどう思われているかなんてことはまったくもって知ったことではない、どうでも良いことだ(もちろん結果として好かれていればさらによりうれしいものだが、それは自身の人生の本質とはまったくもって言えない。)と捉えられれば楽になる。すべての人から好かれることは社会としてむしろ健全なこととはいえない。((人生レベルにおいて)自分自身に理解されることをより積極的に重視した(自分自身が納得できる)、真実の人生を全うするためには)時として嫌われる勇気は『必要悪』だ。
また自己嫌悪というものはうつ病のトリガーにもなりうるので特段の注意が必要である。そういう場合には、私には腹にくくった(決意の一本)槍(やり)として命をかけられる○○(人生を全うするための大切な固有(関数)ベクトル空間)があり、(慣性力をそのままに)そこを突き進められているのならば(その瞬間において)自分のことが好きか嫌いかなんてことはまったくもって知ったことではない、どうでも良いことだ(もちろん結果として好きであればさらによりうれしいものだが、それは自身の人生を全うするための本質とはまったくもって言えない)と捉えられれば楽になる。(その瞬間において他人に理解されることよりも、(人生レベルにおいて)自身自身に理解されることをより積極的に重視した(自身が納得できる真実の人生を全うするためには)時として嫌われる勇気は『必要悪』だ。
これに関して(あるいはわれわれの人生のさまざまな意思決定の場面(シーン)において)ビュリダン(ブリダン)の驢馬(ロバ)の寓話(ぐうわ)は多くの示唆(しさ)を与えてくれる(ロボットの運動学における意思決定の問題においてもよく引き合いに出される)。自身の野性・野能を磨いて『(時として)他人から嫌われる勇気(必要悪)をもって自分の欲する所へゆき、自分の欲することをなす(真実の人生を生きる)べき』であろう。二兎を追う者は一兎をも得ず(迷いがある人間は弱い!)、右のエサをとるか、左のエサをとるかの2択ではなく、その上位にある(どんなエサであろうが取りたいエサを取りにゆくという)決断をする(ことによって覚悟をさだめ、迷いをなくす!)かしないかの2択(胆力:たんりょく)こそが生存(survive)するうえで本質的かつ決定的に重要である。餓死(がし)してはたまらない、、、
(例)コロナ禍は医療のデジタル化においては、けっして悪いことばかりではなかった。これまで、対面診療一択であったところが、オンライン診療やその先にある、AI・ロボティック診療といったところが現実(実用)的な医療提供手段の選択肢としてまじめに検討されるようになってきた。どのような診療形態(モダリティ:modality)であろうが、質の高い医療を破綻(はたん)させることなく安全・安心・安定的に( Me-DigIT 魂のこもった!)思いやりをもってサステナブルに提供しつづけることができるかできないかの2択(胆力:たんりょく)こそが患者の生存(survive)にとって本質的かつ決定的に重要である。
(例)意思決定を行なう際には、現在対象としている階層からひとつ上位のメタ(抽象)的な階層に昇ってみて、あるいはそこから横に半歩ずれてみて、さらにはそこでのコンビネーション効果をも包含した意思決定をおこなうことをも検討してみてもよいだろう((実装)解(零)空間を拡げて考えてみることが戦略的にきわめて重要である!)。なぜなら現在直面している問題の根源が、いつも目の前に顕在化(けんざいか)しているわけではなく、(階層や次元の異なる)思いもよらないところに(特性根や(実装)解として!)存在している可能性は多分(たぶん)にあるからである(問題の特性根や(実装)解はときに思いもよらぬところに存在する!)。
(例)エミー・ネーターが研究を通じて道しるべとした行動原理は、つぎのようにまとめられるだろう。
『数や関数や演算どうしの関係性(つながり、コミュニケーション・リンク、そこで働く超偉大なるテンション(超万有引力!))を明瞭化して、統一(一貫)・統合(包括)的に適用できるようにし、その生産性を最大限に引き出すには、それを特定の対象から切り離して、普遍・一般・抽象的に有効な(メタ的な)概念として(再)表現しなおさなければならない。』
そうしてこのオブジェクト指向的な行動原理は、デジタル化ときわめて相性が良いのである!
(参考文献)
イアンスチュアート,数学の真理をつかんだ25人の天才たち,ダイヤモンド社.
(例)ラーメンとそばを食べるかで悩んでいるときには、その上位にある麺(めん)類を食べる(ああそうか、自分は麺類を食べたかったのか!)というメタ的な概念を考えて、さらには和・洋・中に展開すれば、うどんにしてもよいし、パスタにしてもよい。さらには、コンビネーション効果を考えて、健康のためにサラダもついたうどん定食を食べるのも選択肢としてアリだ!さあてどれを食べようか、、、
目の前の人が自分に対して怒っているときには、自分自身が原因である可能性もあるにはあるが、どこかからぶつけられた怒りをそのまま自分に転化(てんか)してぶつけてきている、言わば『八つ当たり』の『とばっちり』である可能性も多分(たぶん)にあるからだ(『目の上のたん瘤(こぶ)』よろしく、そのほとんどは単なる地政学(的リスク分析)によって説明できる!)。これを真に受けるべき理由など全くないのである!
ためしに10円玉を5枚並べて、端っこの10円玉をはじいてみよう。反対側の端っこに置かれた10円玉が吹き飛ばされることに気づけるはずだ。はじかれるのを避けるためには、たとえば10円玉をボンド(絆)でくっつけ(ることによって機械的なパラメータ(慣性・粘性・剛性)を変化させ)る手がある※。これは人間社会においてコミュニケーション・リンク(およびそこで働く超偉大なるテンション(超万有引力!))をうまく活用してセキュリティ・ネットワーク化する(同盟を組む(Nコイチ戦略をとる!)ことで機械的なパラメータ(慣性・粘性・剛性)を変化させる)ことの重要性を如実(にょじつ)に示している(Groundを大きい所にとることで、機械的なパラメータ(慣性・粘性・剛性)が変化・変容してノイズの影響は低減しうる!そういった感覚・イメージをもっておくことが何かと地政学の影響に暴露(ばくろ)されやすいわれわれの人生戦略上も有効であろう)。
将棋の格言に『金底の歩、岩よりも堅し(きんぞこのふいわよりもかたし)※』というものがある。囲碁と同様、将棋においてもまた、コマとコマとの間のコミュニケーション・リンク(およびそこで働く超偉大なるテンション(超万有引力!))をつくり、取られたら取り返すことができる状態にしておくことが戦略上、あるいは安全保障上、きわめて重要な作業になる。サルの世界でさえ、仲間のサルが殴られれば、仲間が殴り返しにゆくのだという。特に将棋の解説では『(あるコマにある)コマを紐(ひも)づける』という言い方が用いられることが多い。
※運動学的にはなに(がし)かを掴(つか)めば(あるいは手放せば)機械的インピーダンス(慣性・粘性・剛性)が増大(減少)し、固定・安定化(機動(きどう)・非安定化)できる。『溺(おぼ)れる者は藁(わら)をもつかむ』、『転んでもタダでは起きるな(武器になりそうな石っころでも拾っておけ)』の精神!であり、そのようなイメージ、感覚を持っていることがわれわれにとって人生戦略上も有効であろう、、、
(参考文献)
Julia Cameron, ずっとやりたかったことを、(そこに固有値があるのであればたとえいくつになっても)やりなさい, サンマーク出版.
有本 卓, 関本昌紘, 巧みさとロボットの力学, 毎日コミュニケーションズ.
Living with your own unicorn (original color) !
好きこそ物の上手なれ
Who likes not his business, his business likes not him.
と考えるからだ。すなわち、
天賦・天性の『野性・野能(というエンジン)』と『知性・知能(というエンジン)』とは双対かつ相補的な『互いに(テコとなり)互い(のエンジンの固有値)を高め合う(超偉大なるコミュニケーションによって互いにリンクさせることでモーメントを与え合い、時には(バチバチと)化学融合反応(イノベーション)を産み出すべき)』関係にあるというモノの観方・考え方・捉え方・発想の仕方・世界観である!
『(広義の)知性・知能』の位相構造:
『感性・感能』⇔『野性・野能』⇔
『(狭義の)知性・知能』⇔
『悟性・悟能』⇔『理性・理能』
人間の教養とは野性・野能を失うことではなく、(知性・知能との超偉大なるコミュニケーション・リンク生成によって)野性・野能を(変化・変容・)洗練(・進化)させることである(知性・知能との超偉大なるコミュニケーション・リンク生成による野性・野能の変化・変容・洗練・進化法)。
岡部伊都子
数学というものすごく厳密な学問においてさえ、究極のところ正しいか正しくないかは直観(幾何学、野性)的信念に頼らざるを得ない(玉野研一, なっとくする無限の話, 講談社)
背理法を認めるヒルベルトらの形式主義では証明できるが、ブラウワーらの直観主義では証明できない数学の問題が存在する。 数学的存在と物理的存在の間には大きな乖離(かいり)が存在することに今一度留意されたい。
a^bが有理数となるような無理数a,bが存在することを証明せよ
(参考文献)
正しいか正しくないかを最初に判断しようするとビュリダンの驢馬(ロバ)よろしく迷いが生じて動けなくなり、時間を浪費してしまうことには注意が必要である。
間違っていてもよいので自分なりの仮説を立ててみて、それを信じてまずは一歩を踏み出し、とにもかくにも動い(運動し)てみることが得策である(運動を継続している(運動ポテンシャルエネルギーを有している)こと、それ自体に価値がある!)。たとえ誤っていたとしても周囲からの修正(フィードバック、気づき)が必ず得られる(それで十分ではないか!?)。
正しいかどうかより、常に考えているかどうか(常に自分なりの答えが用意できており、即答できる状態にあるかどうか)のほうが現実的に意思決定を行なううえでははるかに重要であろう。
また、せっかく一歩を踏み出したのなら、途中でその歩みを止めるべきではない(運動を継続している(運動ポテンシャルエネルギーを有している)こと、それ自体に価値がある!)。マラソンしかり、寝たきりの病人しかり、歩みを止めた瞬間につぎの一歩を踏み出すことが精神的にも肉体的にも著しく困難になってしまうからだ。せっかくそれまでに少しづつ高めてきた慣性力(運動ポテンシャルエネルギー)を(継続的に)推進力に付加することができなくなってしまい、結果として効率よく(慣性軌道上を)前進(航行)することができなくなってしまうのだ。これは(生命の神髄(クイントエッセンス)を無視した)とてもとてももったいない行為ではないか。
(真実の)人生を全(まっと)うするための固有モード(固有値・固有(関数)ベクトル)に従って、(慣習化して継続的に)走り続けていればこそ、たとえ間違った方向に進んでいたとしてもフィードバックが必ずかかり、少しづつ軌道が修正されてゆく。歩みを止めず(慣習化して運動ポテンシャルエネルギーを維持しながら)どんどんと、とことんまで突き進み、(継続的に)走り続ける姿勢をできうるかぎり維持し、これを定常とすることこそが戦略的にもきわめて価値が高いのである。
(生命の神髄(クイントエッセンス)に従って)突き進み、(サイクリングよろしく継続して)走り続けているからこそ勢いをそのままに、慣性力(運動ポテンシャルエネルギー)を推進力に(慣習化して)どんどん、どんどん添加(てんか)して上乗せしてゆくことができ、結果として効率のよいフィードバックを得ながら(継続的に)前進することもできるのだ。これは固有モード(固有値・固有(関数)ベクトル)に従って『(慣習化して継続的に)とことん突き進む(戦略をとる)人』に対する人生(を全うするため)のボーナス(ご褒美)である!
普通の教師は、言わなければならないことを喋る。
良い教師は、生徒に分かるように解説する。
優れた教師は、自らやってみせる。
そして、本当に偉大な教師というのは、
生徒の心に火をつける。
William Arthur Ward(アメリカの作家・学者・牧師・教師,1921~1994)
(例)高炉は15~20年は生産を続けることを前提に稼働しており、一度休止して火をとめてしまえば再稼働までに長い時間を要することになる。人間の熱意の属性(ぞくせい)も同様なものであろう(だから安易に熱意のTORCH(ともしび)をたやすべきではない)。
(例)マグロは泳ぐのを止めると窒息してしまうため、いっときも休むことなく泳ぎ続ける必要がある。
(例)ターゲットにロボットを追従させようとするとき、慣性力にもとづくターゲットの現在の速度(運動)を予測して、同じ速度(運動)で動かなければどうしても差をつけられてしまう。このとき位置のフィードバック制御のみを実装したのでは、ターゲットとの位置の偏差が生じてこれをまずは観測してからでないとロボットは一歩も動けない(しかしながらこれでは、追従ターゲットにどうしても差をつけられてしまう)。
これに対してフィードバック制御に加えてターゲットの慣性力にもとづく速度(運動)をうまく予測することができれば(まずは、等速直線運動を仮定して1次近似で予測をすることが簡便かつ有効である)フィードフォワード制御(2自由度制御とよばれる)を実装することで追従ターゲットとの偏差が生じる前にロボットは追従動作を開始することができる。
人工知能援用医療ロボットによる臓器内に埋め込まれた患部の追従においてもこれは同様で、慣性力のみならず呼吸に応じた横隔膜の概周期的な運動をも考慮して臓器の速度(運動)を高精度に予測できることが追従戦略上、きわめて有効かつ重要である。
(参考文献)
Motoyasu Sano, Norihiro Koizumi, Yu Nishiyama, Jiayi Zhou, Takumi Fujibayashi, Momoko Matsuyama, Miyu Yamada, Tomohiro Ishikawa, Arashi Katsuragi, Sho Monma: Construction of organ rotation estimation system using deep learning, 37th International Congress and Exhibition on computer assisted radiology and surgery (CARS 2023), International Journal of Computer Assisted Radiology and Surgery (IJCARS), Vol.17, Suppl.1, pp.S98-S99, 2023. https://doi.org/10.1007/s11548-023-02878-2
(例)本を読むときの姿勢も同様である。わからない『点』がいくつか現れることはむしろ通常の(健全な)ことであり、その都度、いちいち立ち止まっていたのでは、せっかくの慣性力(運動ポテンシャルエネルギー)をうまく活かしきれているとは言えない。まずは述べてあることを『点』として記憶しておいて、慣性力(運動ポテンシャルエネルギー)を活かして先に進むべきであろう。そのうえで適当(適切)な時期に読み返したり、その『点』の近傍を詳しく説明している書物にあたることで、『線』あるいは『面』としてしっかり・くっきり・はっきりと理解できるようになることを目指すべきであろう。
テキストや論文など、難解な文章を読むにしても、まずは大局的な文脈を把握(掌握)するための感性・感能(視覚野と超解像度の補間的想像力)に頼った読み方から、局所的な筋道についても国語的・数理的・情報科学的な論理に基づいて精密・精確に深掘り検証するための理性・理能的な読み方まで何パターンか用意しておいて、これらをTPOによって使い分けることが効果的であろう。
(例)UNet(深層学習による超強力な医用画像処理のモデル)は一は全、全は一的画像(絵画!?)の把握・読解(解読)・解釈法か!?
部分(部分画像、パーツ、原子、分子、パラグラフ等)的事実関係(ファクト)の把握⇒(把握した)部分的事実関係のAND演算(掛け算)⇒全体的構図(構造、状況、ゲシュタルト)の把握⇒(世界観の構築/変化:当初とは世界が違って見えてくるかも、、、)⇒全体的構図(構造、状況、ゲシュタルト)の読解(解読)・解釈(もちろん絞り込めず、複数(解)読解という状況もありうる)⇒部分(部分画像、パーツ、原子、分子、パラグラフ等)の読解(解読)・解釈(もちろん絞り込めず、複数(解)読解という状況もありうる)、、、
難解で込み入った文章になればなるほど、1度ですべてを理解できる場合などほとんどないであろう。このような時には芝生を刈るように、何度も何度も繰り返し繰り返し刈(か)る(読む)ことがきわめて有効である。テキストを7回繰り返して(ぐるぐる巻きに)読むことをルーチンにしている人もいるという(さらには魏(ぎ)の董遇(とう ぐう、2世紀後半 - 3世紀前半)が弟子に何度も(ぐるぐる巻きに)読書することの必要性を説いた読書百遍(どくしょひゃっぺん)※という熟語もある!)。泥臭(どろくさ)くても、まずは高い芝、つぎにもうすこし低い芝をと何度も何度も(ぐるぐる巻きに)繰り返して刈(か)る(読む)ことが有効である。
これは、『カギとカギ穴』よろしく、画像などのデータ(カギ)をひっくり返して鏡像(カギ穴)をつくって重ね合わせながらさまざまな階層(レベル)・解像度で(ROI(関心領域)のサイズを変更したり、折りたたんだりしながら、ぐるぐる巻きに)読み込み、テクスチャ(模様)や形状の一致度を見るために画像(の片割れ)どうしをひとつのベクトル(われわれはこれをMe-DigIT画像ベクトルと呼んでいる)とみなして、その内積をとったり(完全一致していれば、内積の値はそのベクトルの大きさ、すなわちノルムの自乗になっている!)、(時間的・空間的・人間的に)フォーカスをずらしたりしながら足しこんだり、(ぼかしてみたり、エッジを強調してみたり、入力画像(カギ)ベクトルに応じていろいろさまざまなフィルタ・カーネルを画像特徴(量)重み(勾配)(カギ穴)ベクトルとして創(つく)りながら、これを学習・調整してゆく(ぐるぐる巻きの!)畳み込みニューラルネットワークによる深層学習の方法と類似(analogous)である。すなわち、深層学習においてもまた、かつて1800年前に魏(ぎ)の董遇(とうぐう)が弟子に何度も(ぐるぐる巻きに!)読書することの必要性を説いた読書百遍(いや、700年前の知恩寺の八世善阿空円上人による百万遍(ひゃくまんべん)というべきか!?)という古典的かつシンプルな戦略が(奇跡を起こすうえでも!)きわめて有効かつ強力だったということである。
Get the Me-DigIT ROLLING, ROLLING, AND ROLLING !!!(われわれの場合)
(ぐるぐる巻きの!)畳み込み積分は内積(ないせき)という演算のもつ特長をうまく援用(えんよう)した処理と言えるが、外積(がいせき)のもつ効用についてもここで今一度、留意(りゅうい)しておこう。数学的には内積は面内の2つのベクトルの並進(姿勢)一致で極大化(cos(0)=1)するかけ算であるが、力学的に力(F)・位置(移動)ベクトル(dx)により仕事(量)(これはエネルギーの単位をもつ)を表現するのに好都合な演算としてまずは導入された。
他方、数学的には外積(がいせき)は面内の2つのベクトルが直交することで極大化(sin(π/2)=1)するベクトルどうしのかけ算であるが、力学的にモーメント(トルク)=(回転中心から力が印加される点までの位置ベクトル(r))×力(F)を計算するのに好都合な演算として導入された。モーメント(トルク)が加わると回転の運動量(角運動量)が変化する。かけ算の結果として得られるベクトルは面外の法線(2つのベクトルの方向を一致させる操作を行なう際に使う回転軸)方向(右ねじが進む方向が正)を向いている。
力学的にまとめると、2つのベクトルの片割れを位置(移動)ベクトル、もう一方の片割れを力と捉えた場合、並進力のなす仕事(量)が内積で(ポテンシャルあるいは運動)エネルギーに変化をもたらし(逆に、エネルギーを潜在的な仕事能力(量)として(再)定義することもできる)、回転力(モーメント、トルク)が外積で回転の運動量(角運動量)に変化をもたらす(もちろん、回転運動のエネルギーは、たとえば電気自動車のモータ(回転子)のように回転力(モーメント、トルク)と回転量(角度、ラジアン)の内積によって潜在的な仕事(量)として表現することもできる)。
『必要は発明の母』よろしく、内積や外積をはじめとする数学的概念は、もとはと言えば物理的現象を明解に説明したいがために導入されてきたものである。この点にはつねに留意(りゅうい)が必要であろう。内積・外積よろしく、本を読むときにも、行(面)内のみならず、行(面)外(間)を含めて心眼(しんがん)を以(もっ)て読む(ベクトルに次元を入れて空間として複眼的に捉える!※)ことができるならば独自の創造(想像)空間が無限(次元)の大いなる、限りのない豊かな広がりをもっていることに気づくことであろう。
※ベクトルを未だ次元が定義されていない空間と捉えることもできる。(なんと!)1次元空間上の点の集合たる直線とN次元空間上の点の集合との間には1対1の対応がついてしまうことに留意されたい。
ここで慣性力(運動ポテンシャルエネルギー)も手伝って前者の読み方は後者の読み方に比べて10倍以上のスピードを出せることも頭の片隅(かたすみ)に入れておくとよいだろう(GPUはCPUの数倍~100倍以上の演算速度を出せるのだ!)。変速ギア搭載の自転車よろしく時間があるときには、低速・高トルクモードの減速機(歯車、ギア)で、厳選した素材を念入りにじっくりと深く味わい楽しむ。他方、時間がないときには慣性力(運動ポテンシャルエネルギー)をそのままに、高速・低トルクの減速機に切り替えて読む。このようにTPOに合わせて読み方を自在に切り替えられるようにしておくとより良いだろう。
具体的に高速・低トルクな読み方としては、なるべく感性・感能(視覚野と超解像度の補間的想像力)による図解に頼って次の展開を予想してイメージとして描きながら、その予想が合っているかどうかを答え合わせをするつもりで文章を(ぐるぐる巻きに!)読み進めてゆく方法がオススメである。ここで予想があっているかどうかはさして重要ではない。
予想の際にあれこれと次の展開について頭のなかで映像化しながら(ぐるぐる巻きに!)想像をめぐらすという行為自体にこそ意義があり、自身の創作活動にとってもきわめて有益なのである。一流の通訳者は言葉をただ単に逐一変換しているわけではなく、視覚野と補間的想像力をうまく駆使(くし)して自身の頭の中で超解像度の映像として状況をうまく再構築・再描写したうえで、他言語によってそれをあたかも実況中継しているかのようにTPOH(Time, Place, Objective, Human)に応じて臨機応変に説明することで自然な訳をリアルタイム(制限時間内)かつ高速に創り出してゆくのだという(たとえ間違っていてもよいからしっかり・くっきり・はっきりとしたイメージをまずは描こう(これが人生戦略上最も有効だ)!そうすれば何らかのフィードバックがかならずかかるからだ)。
このあたりの技法は一流のスポーツ選手の視覚野の働き、お笑い芸人の話芸、作家の創作活動ともまた、相通じうるべきものであろう。すなわち視覚野を単なる目でみた映像を処理する装置としてのみ使うだけではきわめてもったいない。GPGPU(General Purpose computing with Graphic Processing Unit)よろしく、工夫によってさまざまな用途に応用展開する(される)べきものであろう(日頃から考えつづけていた課題で、散歩をしているときや、電車に揺られているとき、シャワーを浴びているときなどにふとすばらしい解決策が浮かぶことがある(セレンディピティ:serendipity)のも、潜在意識レベルにおける視覚野がGPGPUとしてずっとずっと(ぐるぐる巻きに!)働いてくれている(読書百遍!ぐるぐる巻きにめぐる慣性力がもたらす奇跡の成(な)せる業(わざ)の)おかげであろう。そうしてこのようなセレンディピティの感覚・イメージを常時もっておくことが人生戦略上もきわめて有効であろう)。
Get the Me-DigIT ROLLING, ROLLING, AND ROLLING !!!(われわれの場合)
(例)DNAの進化の歴史を紐(ひも)解けば、野性において獲物を抽(検)出して追従する、あるいはモニタリングするという、視覚野におけるリアルタイムな追い駆けっこの高速演算処理を人類を含む動物が生存するために永(なが)きにわたって延(えん)々脈(みゃく)々累(るい)々と(ぐるぐる巻きに)繰り返し行なってきたことに気づく(すなわち、追い駆けっこは生命活動において本質的行動である)。
この事実を踏まえれば他の野性動物と同様に人間の脳においても感性・感能(視覚野と超解像度の補間的想像力)に頼ったほうが理性・理能に頼るよりも、より高速に大量の演算を(ぐるぐる巻きにして!)一度にこなすことができるということにも得心(とくしん)がゆくであろう。
(例)危険を察知するという点では、音(聴覚野)の役割もきわめて責任重大であり、見逃す(いや、聞き逃すというべきか!?)ことはできない。音は、外耳→中耳→内耳→蝸牛神経(聴神経)→脳幹→一次聴覚野(側頭葉)の順に伝わる。動物は、太古の昔から、オオカミの遠吠えなど、危険な音を聞き分けて、危険から遠ざかる(距離を置く)ように行動してきた。人間においても同様であり、さまざまな音によって不安や胸騒ぎを敏感に感じとる(感じとってしまう)場合も多い。
超音波診断においては音の反響を視覚化することでコンクリートの亀裂や臓器内に埋め込まれたさまざまな病変部位を直観的に見通しよく捉えることで危険を察知している。あのおいしい、森永製菓のチョコジャンボモナカのパリパリ感も音(聴覚野)の役割・演出によるところがきわめて大きい。これを踏まえて同社では『心の健康』に寄与する菓子食品のおいしさや楽しさといった情緒的価値を様々な手法で解明し、付加価値の高い商品の開発・提供につなげていく取組みを行っている。
(参考文献)
(例)お笑い芸人などのプロの噺家(はなしか)はシーンを頭に描きながら、いままさにその場にいるかのように話をすることができるという。言語中枢(げんごちゅうすう)にある言語野(げんごや)のみならず視覚野におけるリアルタイムな追い駆けっこの高速演算処理をも言語処理へと応用展開することで感性・感能(視覚野と超解像度の補間的想像力)に頼った話し方がうまく機能している一例と言えよう。直観的なイメージを描けることは生産性を向上するうえでかくも重要である!
健全な精神は健全な肉体に(こそ)宿る
古代ローマの詩人ユヴェナリウス
強なくして用なし、用なくして美なし、美なくして建築ではない!
ウィトルウィルス(2000年前のローマの建築家)が建築十書において
感性⇔(マクロレベルでの)物理的現象
理性⇔数学的現象
感性と理性の間には鋭い亀裂(きれつ)・乖離(かいり)・懸隔(けんかく)が生じて当然であると考えよう。その際、その時々においては(クイントエッセンス(生命の神髄)たる)感性に理性を従わせるほうが人生戦略としては賢明であろう(感性ファースト)。なぜなら感性は(多かれ少なかれ)慣性を有している(1(あるいはN)次遅れ系である)からである。このため急激な変化には即座に(instantly)対応・追従することができず、理性に感性を従わせようとすれば時に精神のバランスが崩壊してしまうことにもなりかねないからである。
(例)都会の時間は田舎の時間よりも早く流れ、時にせわしないと感じてしまいがちである。またそのことが知らず知らずのうちに無言のプレッシャーを都会の人間に与え、日々の生活に疲れを感じさせる一因となっているのかもしれない。
具体的に都会の風景には田舎の風景に比べて、人の流れや土木工事の音など、さまざまな変化・動きがあり、人間の五感がその変化・動きという刺激に引っ張られ(アトラクトされ)、それらをいちいち捉えて、そこから時間の経過を無意識のうちに推察してしまいがちである。
こういう時には精神衛生上、耳栓をして目をつぶる(アイマスクをする)図太さをもつのが吉(よし)である。日光東照宮の叡智(えいち)の三猿(さんざる、さんえん)よろしく時にはまた、あえて『見ざる聞かざる言わざる』に徹っして英気を養うことも必要だ。(英気を養うための時にはあえて『見ざる聞かざる言わざる』法)※
※
人間が視覚から得る情報は全体の83パーセントと言われている。したがって、1分間、目をつぶるだけでずいぶん脳を休めることができる。
(参考文献)
大平信孝,やる気に頼らず「すぐやる人」になる37のコツ (科学的に先延ばしをなくす技術) ,2021.
すなわち理性では一歩前進できるところであったとしても、感性に従ってあえて鈍感に、はやる気持ちをおさえつつ半歩の前進にとどめておく、言わば『(日本人初のメジャーリーガーの野茂英雄投手よろしく!)戦略的スロー・スターター(1(あるいはN)次遅れ系)』であるほうが賢明なのである!他方、中長期的な観点からみれば理性によって感性を少しづつ変化・変容・洗練・進化させることを検討してみてもよいであろう。ロボティック超音波医療診断においてもまた、プローブと患部の間の接触安定性を確保して、音響陰影の少ない好適な画像を得たいがために、その先端機構部をばね・マス・ダンパによる1(あるいはN)次遅れ系で構成している。
われわれは何事においても(もちろん人生においても!)その本質・骨格が低周波成分にこそ顕(あらわ)れる(そうして、その本質・骨格に沿って進む鈍感力が重要である!)ことを経験的に知っている!そうしてそれらは、sparseにmodelingされうる!すなわち、直観的(幾何学、野性的)に見通し良く単純・明解でありうる。
(例)習うより慣れよ
その場合においても、あくまで(われわれを物理的に拘束・支配している)慣性の法則に従いながら少しずつである(精神のバランスを崩してはならない!健全な精神は健全な肉体にこそ宿るのだ!そうして肉体は慣性の法則による制約を受けるのが宿命である)。慣性ゼロの画像追跡処理による追従(ただし、画像とりこみや画像追跡処理にともなう位相(の)遅れは生じうる)に対してロボットによるフィジカルな身体性をともなう追従では慣性の分だけ位相が遅れてしまう(1(あるいはN)次遅れ系な)のだ!(生命の神髄(クイントエッセンス)たる)感性は慣性の分だけ理性よりも(若干:じゃっかん)スロー・スターターなのだ!
新幹線やF35戦闘機でさえ慣性・粘性・剛性といったインピーダンス・パラメータによる運動の拘束からは逃れられず、徐々に加速/減速せざるを得ないのである!(運動ポテンシャルエネルギー(慣性力)を落としてしまう原因となる)急発進や急ブレーキは危険である(慣性力で中身がペシャンコになってしまわないように助走(準備運動)期間を適切に設けるなど何らかの工夫・配慮をする必要がある)!
道路のカーブ形状を設計する際においても、(運動ポテンシャルエネルギー(慣性力)を落としてしまう原因となる)急加速・急減速が生じてしまわないように微分・積分を用いた安全・安心・安定的に( Me-DigIT 魂のこもった!)思いやりを持って軌道を計算することで事故の大幅な減少につながっているそうである。具体的にはハンドルを一定の速度で切って、一定時間維持して、一定の速度で切り返せば(運動ポテンシャルエネルギー(慣性力)を極力維持しながら)首尾よくカーブが曲がれるように道路のカーブ形状はきわめて合理的に設計されているのだそうである。
医療・バイオ・福祉ロボットのように生体に接触して動作(相互作用)するロボットを安全・安心・安定的に( Me-DigIT 魂のこもった!)思いやりを持って運動(軌道を)制御(motion control)する際においてもこれは同様であり、インピーダンス(機械的パラメータ:慣性・粘性・剛性)の制御はきわめて重要である!機構部の振動を極力小さくするためのパルスモータのS字加減速制御などを参照されたい。
理性は慣性・粘性・剛性(機械的パラメータ、インピーダンス・パラメータ)やプランク定数(h =6.6261×10-34ジユール・秒)の制約から開放されているため、その変化・変容は数学的現象として随意(自由自在、at will)である。このため、感性に理性を従わせることは造作(ぞうさ)もないことに着目されたい。
他方、理性に感性を従わせることは一般に少なからず困難をともなう場合が多いということをわれわれは経験的に知っている(慣性・粘性・剛性のあるロボットが環境によっては思い通りに動かずに、特に高速な運動を行なわせようとすると幾何学に基づいた運動学に加えて慣性・粘性・剛性、さらには遠心力、コリオリ力、並びに曲率項※(centrifugal force)まで考慮した動力学に基づいたより高度な制御理論が必要になってくる所以(ゆえん)でもある!また車やバイク、電車などが急には止まれず、子供の遊びで落とし穴(pitfall)が、サッカーやバスケットボールなどのスポーツ競技においてフェイント動作(feint operation)が有効に機能する理由でもある!)。
※遠心力、コリオリ力、並びに曲率項はいずれも角速度ω 一定の回転座標系(遊園地のコーヒーカップの乗り物のイメージ)に対して現れる慣性力の一種である。
(参考文献)
https://humans-in-space.jaxa.jp/faq/detail/000706.html
(例)プランク定数
h =6.6261×10-34ジユール・秒をほとんどゼロとみなしうる(エネルギーと代表的な運動周期との積ET>>hであり、無限の相(分割)(ET/h~∞)を仮定しうる十分に『アナログ的』な)力学系では力学的現象をニュートン力学でハンドリングしたとしても大きな齟齬(そご)は生じない。
他方、原子内の電子のエネルギーEは10-17Jの程度で公転時間Tは10-16sの程度と極小であるのだから,その積ET~hとなり(物理的限界として、もはや無限の相(分割)を認めることは困難な状況となり)ニュートン力学との大きな乖離(かいり)が生じてしまうためこれを適用することにはこの世の現象を説明するうえでどうしても無理が生じてしまい、(有限の相でデジタルにハンドリングしうる)量子力学というあらたな力学系(世界観)を導入する必要がある。
物理学博士の友人によれば物理学者のスタンス(stance)はまさしくこのスタンスであり、数学の健全なる部分を扱うのが物理学者であるという。他方、数学の病的なる部分の扱いについてはありがたいことに蛇(じゃ)の道は蛇、餅(もち)は餅屋で数学者が担(にな)ってくれているのである。
数学的現象も物理的現象もいずれも人間の直観(幾何学、野性)的信念をその起点・原点・出発点(starting point)・一丁目一番地・基礎・基盤・土台・土俵(infrastructure)・根本・根幹とするが、枝葉花(果)実については論理的矛盾がないのであれば自由な発想のもとで新たなモノを創造し、随意(自由自在、at will)に展開しうるというのが数学者のスタンスであり、数学のプロの世界観である。数学の本質はまさにその発想の自由さにこそある!
(例)数学といえども絶対的真理とまではいえず、ある公理(系)(明示されたいくつかの前提となる命題(数学的主張、ユークリッド幾何学の場合は5つ))を基礎・基盤・土台・土俵・インフラストラクチャーとして人間の直観(幾何学、野性)的信念にもとづいて定めた後、そこから導出される真理(命題や定理)の集合をまとめたものにすぎない(公理的集合論)。
(例)論理性に立脚する数学は、定義・定理が重要で、わずかの矛盾も許容されない。果たしてそれが絶対的真実であるのか、ある条件(土俵、台、定義域)のもとでのみ成立する事柄であるのかは十分に検討し尽くされなければならない。三角形の2辺の和が他の一辺よりも大きいという主張は、非ユークリッド空間においてはとても鵜呑(うの)みにはできない主張となってしまう。
(参考文献)
都筑卓司、トポロジー入門、講談社.
(例)数学においてもその進化の歴史を紐(ひも)解けば、まずは直観(野性)的信念にもとづくユークリッド幾何学が発達する。数学という学問を生み出した人類がDNAの進化の歴史のなかで長い間、野性・野能をその根本・根幹にしてきたのだから当然といえば当然である。
つぎに17世紀のルネ・デカルト(René Descartes、1596年3月31日 - 1650年2月11日)およびピエール・ド・フェルマー(Pierre de Fermat、1607年10月31日から12月6日 - 1665年1月12日)による座標系の発明により、幾何学的図形が数式で表現され(座標系には直交座標系、極座標系、円筒座標系などさまざまある)、 代数学と結びつく(解析幾何学とよばれる)。直線や平面(さらには一般のn次元ユークリッド空間に埋め込まれた(超)平面、平(たい)らかな空間)を1次(線形方程)式で表現することこそ(1次)線形性の認識の起点・原点・出発点(starting point)・一丁目一番地である。※
※『(原点を通る(斉次な))直線』を同じく、『(原点を通る(斉次な))直線』に写す、『線形写像(の学問)』が『線形代数学(linear algebra)』という学問の名前の由来であり、その名称からは浮世絵(うきよえ)のごとく美しく甘美(かんび)で洗練された抽象的な雰囲気こそ感じられるものの、その抽象さゆえにいささか素人にとっては足場がフワフワとしたものに乗っている感じがするかもしれない(何をするにしても足場(基礎・基盤・土台・土俵・インフラストラクチャ)がしっかり・くっきり・はっきりとしていることは重要だろう!)。
このように感じられるときには線形結合、線形独立は1次結合、1次独立といった具合に『線形』を『1次』で読み替えるほうが、多少泥臭くは感じられるもののわれわれにとっては工事現場よろしく、より具体的で足場がしっかりしている感じがして直観・幾何学・野性的に見通しよく、単純・明解に理解ができ、安全・安心・安定的で( Me-DigIT 魂のこもった!)思いやりがあり、腑(ふ)にも落ちやすいであろう(あるいは抽象化の流れと、具体化の流れとを併せて表現した『線形1次』という呼び方も如意金箍棒(にょいきんこぼう)よろしく絶妙(ぜつみょう)であろう)。
余談だが、デカルトは座標系の発明を論文として発表したが、フェルマーはしなかった。このため、現在の座標系はフェルマーが考案したものにより近かったにもかかわらず、デカルトの座標系とよばれることが多い。本来はデカルト・フェルマーの座標系と呼ぶべきであろう。デカルト座標系は英語ではCartesian coordinates(カーティジアン・コッ・オーディネッツと発音)と呼ばれる。
デカルトの『デ』が入っていないので、日本人が国際学会などで話す際にはあやまって『デ』を入れて発音してしまわないように気をつける必要がある。私も初めての国際会議発表でひとつ前の発表者が『Cartesian coordinates』と話しているのを聞いて、『デカルトの座標系』のことだとその場で気づかなかった覚えがある。『Hamiltonian』も『ヘイマルトニアン』と発音する。カタカナ英語は罪つくりである!
最後に、上記の座標系の発明による幾何学と代数学との間のコミュニケーション・リンクおよびそこで働くテンション(このコミュニケーション・リンク、超偉大なるテンション(超万有引力!)は『万有引力』を発見したニュートンによって解析幾何学と命名された)が契機となって化学反応をともなうイノベーションが起こり、相互にモーメントを与え合いながら18世紀に(1次)線形代数学、微分積分学、(世界でもっとも美しいと称されるオイラーの公式、恒等式をはじめとする数学界における至宝、『世界遺産』たる絶景の宝庫である!)複素解析学などの分野が急速に発展する(近年ではさらに数値計算によるデジタル化の流れも上記に加わる)。複素(ガウス)平面は極座標との相性が良く、ひとつの複素数で原点まわりの回転と原点を中心とする伸び縮みを直観・幾何学・野性的に見通しよく表現することができる。
リー群(多様体)およびその接ベクトル空間であるリー代数の理論は、数学のみならず、量子力学、一般の工学において(もちろんロボティック超音波においても!)本質的かつ重要な概念である。これに付随した有限複素単純リー代数の幾何学的な構造の決定※は20世紀数学における金字塔のひとつであった。
※有限複素単純リー代数における計算には(計算間のコミュニケーション・リンク、およびそこで働く超偉大なテンション(超万有引力!)によって生成される氷の結晶が如き美しい)幾何学的構造にもとづく住み処のパターンがあり、そのパターンの数は(なんと!)有限である!ローレンツ群およびポアンカレ群は特殊相対性理論において時空の等長性を記述するために導入されたリー群で、それぞれ 6 および 10 次元である。ローレンツ変換は内積(距離)が保存される等長変換であり(三角形の合同条件を考えればすべからくして角度(や面積、体積等)も保存されることになる)、ポアンカレ変換はローレンツ変換に並進が加わったものである。
ペアノらが創始した公理的集合論とは、まずは直観(・幾何学・野性)的にみて納得(得心)できる数学的主張(定義、命題、性質)を公理(系)として(無条件に前提として)認めてみて、これを基盤にさまざまな命題や定理を演繹的あるいは帰納的に導出し、さまざまな(数学的)対象についてその性質や属性について議論しようとする、『この指とまれ』の集合論である※。このとき、さまざまな(数学的)対象は空間上の点の集合としてみなしうることから、上記の解析幾何学がその効力を発揮する。
※公理的集合論は数学の分野を書き換え・再構築してきたが、人工知能・ロボットの分野もこれによって書き換え・再構築されようとしている。
ピタゴラスの定理で有名なピタゴラス学派(ピタゴラスが生きていたのはB.C.582-B.C.496年頃だったと言われている)の世界観は『万物は数である』というものであり(彼らのいう数とは自然数とその比である分数(有理数)のことである)、数が自然界、そしてこの世の根本と考えていた(すなわちピタゴラス学派の世界観は実にデジタル的であった!)。
ピタゴラス学派よろしく、長靴に黒板消しにビールジョッキ、サハラ砂漠やアラビア砂漠の砂粒、ナイル川や黄河のひと雫(しずく)など、自然数(や有理数)でナンバリングすれば、ありとあらゆるものごとは空間上の点やその(点)集合としての領域に(デジタルに)対応(写像、マッピング)させることができる。
いったん空間上の点やその(点)集合としての領域にマッピングされればその性質や属性について数学的対象としてさまざまに議論することができるしまた、(この指とまれの集合論的)点群処理によりデジタルに解析・ハンドリングすることもできる。点群処理は医用画像処理においても不可欠なツールとなっている。
砂漠の一粒一粒という構成要素が集まることによって、サハラ砂漠やアラビア砂漠といった特徴的な全体(の構図・構造・全体像)が構築されているという集合論的なモノの観方とアラビア砂漠における砂粒と砂粒の間の関係性や(全体の)構図・構造・全体像(互いに他を磨きつづけている)が一つ一つの砂粒に役割(や輝き)を与え、その砂粒を特徴づけているという構図・構造・全体像論からの2方向からの観方があり、2つの観方は相(あい)並立しうる。
他方で、心理学の父と呼ばれたドイツの心理学者・ヴェルトハイマーらによって提唱された『ゲシュタルト心理学』は人間の精神を全体的に(一塊のブロックとして)捉えることに重点を置いた心理学である。ゲシュタルト心理学の大きな考えかたのひとつに『部分の総和は全体とは異なる』というものがある。人間の知覚であれば、個々の感覚を総合して『個』としての存在があるという訳ではなく、あくまで全体的な枠組み(モデル・型・枠)である『ゲシュタルト(構図・構造・全体像)』があることによって『個』が存在するというモノの観方(認識)・考え方・捉え方・発想の仕方・世界観である。
『ゲシュタルト(構図・構造・全体像の)崩壊』とはまとまった(一塊のブロックとしての)モノ(構図・構造・全体像)がバラバラになっていく感覚のことをよぶ。初めは全体としてひとつの漢字として認識できていたものが、じっと眺めて(個々のパーツに着目して)いるうちに視覚的(金属)疲労(破壊)が起こった結果として、その骨格(こっかく)や枠組(わくぐ)みを失い、その帰結(きけつ)としてバラバラのパーツ(部分部分=構成部分)に見えてきてしまい、結果的に何が何だか意味がわからなくなってしまったり、意識せずに普段おこなっている行動、例えば呼吸や唾を飲み込むといったものが一旦(部分を強く)意識することによってできなくなってしまうという現象が『ゲシュタルト(構図・構造・全体像の)崩壊』の例として挙げられている。野球選手が『部分』にこだわるあまり、ピッチングフォームやバッティングフォーム(構図・構造・全体像)を崩してしまう(イップスなどの)現象も、この『ゲシュタルト崩壊』と関連するのだろう。
バラバラのパーツ(部分部分=構成部分)としてではなく、全体的なつながり(超万有引力!)、枠組み(モデル・型・枠)のなかで物事を捉える(捉えなおす)ということ( Me-DigIT! 超万有引力!)はモノの観方(認識)・考え方・捉え方・発想の仕方・世界観においてかくも重要である(読解や読影といった知性・知能の本質でもある)!地球(地表)の構造・状況を把握する際にも場合に応じて鳥観図や人工衛星図的な視点を臨機応変にとることがきわめて有効であろう!
科学のどの進歩にも完璧な無知からはじまって、証拠にもとづく部分的な知識が(超万有引力!的につながって)しだいに確実になるという段階を経て、事実上確実になるという段階に至るという(複利的)変遷が含まれる(Howie)。
アニメ『鋼の錬金術師』では『一は全、全は一』とは何かと師匠から問いかけられたアルとエドが無人島に放り込まれ、そこでサバイバルするなかで(ぐるぐる巻きの!)万物(ばんぶつ)の流転(るてん)を体感(たいかん)し、世界の真理の断片(だんぺん)を見出した。
(師匠からの問い)一は全、全は一(One is ALL, ALL is One)とは?
(アルとエドの回答)全は世界、一はオレ(ALL is the WORLD, One is Me)
ここで、要素が関係性(コミュニケーション・リンク、超偉大なるテンション(超万有引力!))や(これにもとづく社会)構造をつくる、あるいは関係性や(社会)構造が要素に役割を与えるという具合に、因果関係は互いに逆方向に働いていることに着目されたい。土俵上の技(ユークリッド運動群(技))の上に技を重ねて、なお土俵上の技であり続ける(群の概念)!『有理数全体』の集合は『1』を『たしひきかけわり(線形代数演算技)』することで生成されるのだ。いったん有理数を構成できれば、その極限を考えて実数を、さらにはこれに次元を入れて複素数へと数の世界をどんどん拡大してゆくこともできる!
(例)UNet(深層学習による超強力な医用画像処理のモデル)は一は全、全は一的画像(絵画!?)の把握・(解読)読解・解釈法か!?
部分(部分画像、パーツ、原子、分子、パラグラフ等)的事実関係(ファクト)の把握⇒(把握した)部分的事実関係のAND演算(掛け算)⇒全体的構図(構造、状況、ゲシュタルト)の把握⇒(世界観の構築/変化:当初とは世界が違って見えてくるかも、、、)⇒全体的構図(構造、状況、ゲシュタルト)の(解読)読解・解釈(もちろん絞り込めず、複数(解読)読解という状況もありうる)⇒部分(部分画像、パーツ、原子、分子、パラグラフ等)の(解読)読解・解釈(もちろん絞り込めず、複数(解読)読解という状況もありうる)、、、
水や空気が流れることによって創り出される紋様(もんよう)であり、錬磨(れんま)された、一粒一粒がその構成要素となっている美しい砂紋(さもん、Ripple marks)は自然が創り出した絶景であるが、その裏には上記の双方向性が働いていることに気づく。我々一人一人と社会との関係も似たようなものかもしれない。ちなみに砂紋(さもん)がそのまま化石となったものは漣痕(れんこん)と呼ばれる。
(参考文献)
柳谷 晃,天才数学者たちの超・発想法,大和書房.
藤田博司,集合と位相,技術評論社.
菊池 誠,公理という考え方,数学セミナー,Vol.71, No.8, 2022.
ダフィット・ヒルベルト(David Hilbert)は、ペアノらが創始した、公理的集合論を強力に推進、ユークリッド幾何学がベクトルの概念を基盤に現代的な公理によって再構築できることを示した。集合論を創始したのはゲオルグ・カントールであり、ヒルベルトはカントールの強力な支持・信奉者(しんぽうしゃ)でもある。これにより、線形代数学や微分積分学における複雑な公式は極めて直観・幾何学・野性的に見通しの良いものとなり、さらには高次元幾何学の建設までもが可能になった。
ヒルベルト空間は(n次元)ベクトルの概念を基盤にユークリッド空間を高次元あるいは可算無限次元に拡張・一般・抽象化してメタ的な概念にしたものである。これにより、われわれにとって直観・幾何学・野性的に理解しやすい低次元(2次元あるいは3次元)のユークリッド空間における線形代数学や微分積分学の方法論を任意の有限あるいは無限次元の空間(フィールド・土俵)へと自在に拡張・一般・抽象化してメタ的な概念としてこれを持ち込むことが可能になる。
通常の(1次)線形空間には距離が導入でき、そこでは回り道すれば距離は長くなる(三角不等式)。距離空間である(1次)線形空間にさらに内積を実装したものがユークリッド空間である。距離が定義された(1次)線形空間を高次元あるいは可算無限次元に拡張・一般・抽象化してメタ的な概念にしたものがバナッハ空間、これに内積を加えて計量まで可能にしたものがヒルベルト空間である。バナッハ空間もヒルベルト空間もそれらが発明された歴史的な経緯(けいい)として関数ベクトル空間を強く意識している。
正規直交基底(正交底:せいこうてい)が定められており、その帰結(きけつ)として内積という統一・統合・普遍的な計量手段を具備(ぐび)していることがヒルベルト空間を特徴づけているが、そこでは角度や長さの計量が時間・空間・人間(じんかん)を超えて可能になる。またヒルベルト空間は完備性をも具備しており(完備距離空間)、そこでは極限としての解の存在が保証されているため、微分積分学の装備一式が有効に機能する。
完備(かんび)性に関してオーギュスタン=ルイ・コーシー(Augustin Louis Cauchy, 1789年8月21日 - 1857年5月23日)は有理数のコーシー列が有理数という土俵の枠内には収まりきらず、無理数(と有理数を包含した実数)を析出(せきしゅつ)してしまうことを見出した。すなわち、有理数空間は完備とはいえない。観方を転じてみれば、上記の析出処理によって任意の実数を有理数のコーシー列によって定義できていると捉えることができる。他方、実数のコーシー列については実数の土俵の枠内に収まりきるため、完備であるといえる。上記の事実より、実数空間を有理数空間が埋め込まれた完備化拡張空間と捉える世界観も可能である。
フェリックス・クリスティアン・クライン(Felix Christian Klein、1849年4月25日 - 1925年6月22日)は、公理的集合論の世界観にもとづいて幾何学を『集合に対する変換群の作用』として分類し、変換群における不変的属性および特徴量によって統一・統合・普遍的にハンドリングしようとした(エルランゲン構想)。すなわち、ユークリッド幾何学を合同変換群の作用における不変的属性および特徴量(寄り道をすれば道のりはかならず長くなる距離の属性や内積(距離、角度、面積、体積)等)を扱う学問分野として、射影幾何学を射影変換群における不変的属性および特徴量(寄り道をすれば道のりはかならず長くなる距離の属性等)を扱う学問分野として再定義・再構築しようというのである。
(空間に無限遠点を付加することで、あらゆる2直線は(たとえそれが平行な直線であっても)交わるものと捉える)射影幾何学においても(なんと!)距離を定義することができる。具体的にたとえば、実射影平面上の点を三次元ユークリッド空間の原点を通る直線と原点を中心とする単位球との二つの交点をもちいて、二つの直線間の射影平面での距離を交点間の距離の短いほうとして定義すればよい。
カール・テオドル・ヴィルヘルム・ワイエルシュトラス(Karl Theodor Wilhelm Weierstraß, 1815年10月31日 – 1897年2月19日)が考案したε-δ論法によってはじめて、われわれは連続性(や微分可能性※:Differentiability)というものを数学的に厳密に定義することができるようになった。ワイエルシュトラス以前の人々にとって連続性(や微分可能性)とは、いかに偉大な数学者であったとしても自身の幾何学的直観(野性的信念)にもとづいて理解するべきものであった。
※『(幾何学的に)とんがっているかどうか(特異点)』を扱う微分可能性ついても『1回(階)微分すると不連続性(飛躍:Jump)があらわれる』といった具合に結局のところ『(n回)微分した関数の連続性』の議論に持ち込むことができるので、メタ的には『連続も微分もあわせて(n回)微分した関数の連続性』の議論として統一・統合的に捉えるメタ的な世界観も可能であろう。
連続性に関してリプシッツ連続(Lipschitz continuity)の条件は呼吸・拍動等に応じて能動的に運動する臓器の抽出・追従・モニタリングを行なううえでも有用である。直観的には、リプシッツ連続函数は変化の速さが制限されるときにその最大値Lを与える。即ち、適当な有限値の実数Lが存在して、その函数のグラフ上の任意の二点を結ぶ直線の傾きの絶対値はその実数を超えないと考えることができる。この上界(じょうかい)をその函数の『リプシッツ定数L』(あるいは一様連続度)と呼ぶ。たとえば、臓器の運動は瞬間最大速度L(腎臓の場合は20mm/sec程度)が制限されているため、このLを評価・同定することで関心探索領域(±L_x, ±L_y)の大きさを制限することができ、効率的な臓器の抽出・追従・モニタリングが可能になる。
ところで、『運動軌道がなめらか』とか、『地形がなめらか』など、われわれが人間(マクロ)的な感覚で『なめらか』というときの『なめらかさ(Smoothness)』は、数学で言うところの微分可能性(Differentiability)とはすこし様相(ようそう)に乖離(かいり)があるように思われる。この場合の『なめらかさ』においては、たとえば運動軌道中に高周波成分がどれくらい含まれるか(フーリエ解析)?や形状がどれくらい複雑か(フラクタル次元)?に近い『なめらかさ』の指標が対応するであろう。これに関しては、『テクスチャ解析』などの理論が参考になる。
黒木哲徳, なっとくする数学記号, 講談社.
オイラーの公式
特に、θ = π のとき

となり、この関係はオイラーの恒等式(Euler's identity)と呼ばれる。
しかしながらやはり根っこの土台部分では数学というきわめて厳密な学問においてさえ、直観(幾何学、野性)的信念をその根本・根幹として頼らざるを得ないのである!
他方、枝葉花(果)実部分についても物理的現象に数学的現象を従わせようというのが物理学者のスタンスであり、物理学のプロの世界観である。
(例)モーメントの概念においてもその進化の歴史を紐(ひも)解けば、その根幹部分において直観(野性)的信念にもとづいていることに気づくが、数学者のスタンスとの大いなる違いは枝葉花(果)実部分についても物理的現象に数学的現象を従わせようという物理学者のスタンスにこそある。
具体的にまずは物体を運動させる能力という観点から力を捉え直した『力のモーメント(てこの原理)』の概念を起点・原点・出発点・一丁目一番地(starting point)とする。つぎに、曲げモーメント(はりの軸をグイッと曲げて変形させる能力という観点から力を捉え直したもの)へとモーメントの定義が変化・変容・洗練・進化する。
はりの変形をはじめ、物体の変形をハンドリングする際に用いられる縦弾性係数ははりを直方体※として捉えたときに、面に垂直な方向の単位面積あたりの力(垂直応力)によるその方向(面に垂直な(法線の)方向なのでこの方向は一意に定まる)の変形度合いを表現する。
※直観(幾何学、野性)的に見通しの良い名前のつけ方は重要である。なぜなら誤解を招くこと(コミュニケーション・コスト)が少なくなるからだ。中国語では日本語の『立方体』を『直方体』と呼び、日本語の『直方体』を『長方体』と呼ぶ。2次元の『長方形』と3次元の『長方体』とが対応する中国語式の呼び方のほうが統一・統合・普遍的で直観(幾何学、野性)的に見通しが良いように思われる、、、
(例)正規直交基底(せいきちょっこうきてい:正交底(せいこうてい)と略されることがある)と原点からなる座標系を単に『直交』座標系と呼ぶ。ここで、正規直交の『正規(せいき)』が外れてしまっているところが、線形代数の容易な理解を促進するうえでまことに惜しいかなと思われる所である。また、この流れで正規直交基底を横にならべた行列を『正(規直)交行列』といったほうが、より的確に伝わるところが、(単に)『直交行列』という表現にとどまってしまっている。これでは『片手落ち』であるという非難をまぬかれまい。これを踏まえてわれわれは理解を促進・容易化するために『直交』の文字を『正交』と読み替えるか、『直交』の前に都度(つど)、(心の中で)『正規』を補って読み進めることにしよう。直観的に見通しのよい名前の付け方は理解を促進するうえでかくも重要である!
※はりの変形は、直方体あるいは円柱によっておおよその傾向をまずは簡便に捉えられることが多い。この方法は、テーラー展開の1次近似的な捉え方ではあるものの、変形のオーダーを捉えるうえではそれで十分に有効であることも多い。漫画や絵を描くときにも、まずは、直方体・球・円柱といった簡単化された図形をパーツとして用いて構図や陰影のつき方に関する簡便な検討が行われることが多い。
横弾性係数は面に平行な(接線:tangential)方向の単位面積あたりの力(せん断応力)によるその方向(面に平行な(接線:tangential)方向なので、この方向は2次元の面内で360度方向にさまざまとれる)の変形度合い(ばね定数、材料のこわさ)を表現する。
せん断応力は物体を(仮想的に)せん(切)断する際にその(仮想的な)切断面に平行に働く応力(単位面積あたりの力、この方向は2次元の面内で360度方向にさまざまとれる)のことである。プローブと患部との接触状態に応じて超音波診断画像に変形をもたらすのは、仮想切断面でもあるプローブのスキャン面に平行に働くまさにこのせん断応力である!
このときプローブの押しつけ方向に発生する応力を(面に対して平行(正接:tangent)方向の)せん断応力として捉えるか、(面に対して法線(正対:face to face)方向の)垂直応力として捉えるかは世界観(対象とする応力をプローブスキャン面で捉えるのか、あるいは体表面で捉えるのかといった、捉える面(座標系)の選び方)の問題であり、体表面で捉える場合にはこの力を垂直応力として扱うべきであることには留意されたい。これについてより詳細を知るためには応力テンソルの理論を学ぶ必要がある。当たり前のことかもしれないが、どの面に着目するか(座標系の選択の仕方)によって、(その面に対して)垂直(あるいは平行)に働く応力(成分)は変わってくるのだ。
(参考文献)
高木隆司, キーポイントベクトル解析, 岩波書店, 1993.
ここで、多様体に対する接ベクトル空間よろしく、プローブと患部(多様体に対応)の接触点付近ではその周囲にユークリッド空間を頭のなかにフレームとして設定していることに留意(りゅうい)されたい。このときロボットマニピュレータなどのリンク機構における各リンク間の運動学的な関係を4つのパラメータ(関節角(θ)、リンク長さ(l)、リンクねじれ角(α)、リンク・オフセット(d))を導入することによって記述する方法であるデナビット・ハーテンバーグの記法(Denavit-Hartenberg method)にもとづいて、プローブの押しつけ方向の軸がz軸、スキャン面をxz平面、スキャン面に垂直な方向をy軸とすれば直観的にも見通しがよい。プローブを運動させると、フレームもこれに付随(ふずい)して移動する(moving frame)。
その後、断面2次モーメント(はりの軸方向(z軸)に垂直な(2次元平面上にある)断面の(質量分布の)x軸あるいはy軸まわりの回転のしやすさ(慣性)をあらわす)、断面2次極モーメント(はりの軸方向まわりの回転のしやすさ(慣性)をあらわす)へとモーメントの定義が変化・変容・洗練・進化する。
ここでロボット工学の座標系の取り方(デナビット・ハーテンバーグの記法)と材料力学の座標系の取り方が一般に異なっていることには注意が必要である。ロボット工学の座標系の取り方ではリンクの方向に根元の軸穴から手先の軸穴にむけてx軸をとるのが一般的である。このx軸は材料力学では梁(はり)の長手方向に対応し、z軸とするのが一般的である。
これは回転軸まわりの慣性(質量)の『分布』を表現している。ここで『2次』は(回転軸からの距離)の2乗に比例した値になるという意味で用いられており、1次モーメントは重心、0次モーメントが平均を表す。
近年では、 上記の断面2次(極)モーメントとのアナロジー(比喩、analogy)から『(ある軸(これは画像上の点(極)である)まわりの画像上での輝度あるいは濃度の)分布』を表現する際にもモーメントという言葉が転用され、応用展開されている(画像上の(輝度あるいは濃度)モーメント)。これにも1次および0次モーメントがある。

『暮らし安心クラシアン』よろしく、ガウス積分はまさに神出鬼没(しんしゅつきぼつ)にあらわれる、言わば『お助けマン
( Me-DigIT !)積分』でオーギュスタン・ジャン・フレネル(Augustin Jean Fresnel,1788年5月10日 - 1827年7月14日)が考案した、回折する光の強度分布を計算する際に使用されるフレネル積分 (Fresnel integrals)のなかにもあらわれる。

(参考文献)
さてディラックのデルタ関数δ(x)は言わば、世界のあらゆるものごとの分布、すなわち局在(きょくざい)を表現して、これを抽出(cut out)・再配置(cut in)することができるという、超関数の代表(キャプテン・花形選手・ヘッドライナー)である。超関数の代表選手であるデルタ関数がシュワルツによって電荷の分布と関連づけられたことから超関数のことを英語ではdistribution functionとよぶ。
われわれの医療のデジタル化(医デジ化)関数:Me-δigIT(t,x,h,H)関数(メディジット・ファンクション)もこうありたいと考えており、上記のディラックのデルタ関数δ(x)を時間(t)、空間(x)、人間(h,H)に適用して普遍・一般・抽象化したメタ的な概念として医療への応用展開を志向しようとするものである。
AI・ロボット・IoT技術を援用した医療のデジタル化(医デジ化)により、デジタル空間上のデジタル機能関数として、人体に埋め込まれた患部のモデル化や医療技能のデジタルな蓄積・改良・再利用が可能になり、時間・空間・人間を超越して、医療の偏在(へんざい)を解消、一定水準以上の医療の底上げ・生産性向上につなげることができる。
理解はできるが信じられない!(Georg Cantor, 1877年, 無限の相(分割)を認めれば、平面上(ヒルベルト空間の理論によればこれは高次元あるいは可算無限次元に拡張した一般のn次元ユークリッド空間上であってもよい!why n次元立方体にGeorg Cantorの対角線論法を適用せよ!)の点と直線(如意金箍棒のごとく縮退させた端点を含まない開線分であってもよい!)上の点とが一対一に対応してしまうという結論を自らの手で導いたときに思わず発した言葉。
Je le vois. Mais, je ne le crois pas. 理解はできるが信じられない!
逆に考えれれば、n次元ユークリッド空間上の点の集合を一対一に対応させて直線上の点の集合に縮退させることができる!これは、プログラミングにおいて1次元のメモリ空間(生命の設計図たるDNA情報も1次元のメモリ空間上に記録・収納されている!)上にn次元配列の要素を(縮退させて)表現できることと類似(analogous)である。
ただし、上記の一対一対応における写像表現は、かならずしも近傍の点を近傍に写す連続写像としては表現できていないことには注意が必要である。すなわち、点の連続性とは空間の次元の増加/減少によって(見かけの表現上は)容易に分断/接合(ぶんだん/せつごう)されうる、言わば『次元を超えた、より根本的かつプリミティブなところにある概念』であるともいえる。
(例)非負整数の無限列:[k_1, k_2,k_3, k_4,k_5, k_6,…]と非負整数の無限列の順序対:<[k_1, k_3, k_5, …],[k_2,k_4,k_6,…]>との1対1対応が存在する。
(参考文献)
藤田博司,「集合と位相」をなぜ学ぶのか,技術評論社.
(例)1次元の線分と同一の長さの辺を有する2次元(一般のn次元あるいは可算無限次元であってもよい)の正方形は異なる図形であるにもかかわらず、同一の長さの辺を有するヒルベルト立方体とよばれる(可算)無限次元の立方体との直積をとるといずれもこれまたヒルベルト立方体となり、同相な図形になってしまう。
プランク定数の制約に縛(しば)られる物理的現象にもとづく世界観とこれに縛られず、無限の相(分割)を認める数学的現象にもとづく世界観との間には鋭い亀裂(きれつ)・乖離(かいり)・懸隔(けんかく)が生じうるのである!自然界は、その極限としてアナログ的であることを志向しているようにも見えるが、物理的な存在である以上、(マクロ的にみて)いくらアナログ志向であるといってもやはり、その存在自体はまぎれもなく(ミクロ的にみて)デジタルでありつづけるのである。)
物理学者は生命の神髄(クイントエッセンス)たる直観(幾何学、野性)的信念のなかに正しいか正しくないかの判断根拠を求めるが、数学者はこの生命の神髄(クイントエッセンス)たる直観(幾何学、野性)的信念のなかに何か気づかない前提条件(罠,trap)が置かれ(仕掛けられ)ているにもかかわらず、それがあたかも地雷原(じらいげん)のように一目見てわからないように覆(おお)い隠されてしまってい(るがために論理的矛盾がないにもかかわらず自由な発想の展開やこれに基づく行動(展開)選択の自由が制限・阻害されてしまってい)るのではないか(そしてそのことは実は、とてもとても勿体(もったい)ないことではないのか)!?と(物理学者からみれば時には過剰とも思われるくらいに)心配してしまうものである。
(特に物理学と比較したときの)数学の本質はまさにその(発想の)自由さにこそある
Georg Ferdinand Ludwig Philipp Cantor(1845-1918)
(例)数学はその対象(たとえば対象としての無限たる実無限)とプロセス(たとえばプロセスとしての無限たる可能無限)のいずれにおいても概念的なものである。他方、心理学的にはこれらは区別されている。しかしながら数学的にはこれらは同じ硬貨の表裏であり、プラトンのイデア論よろしく概念的なモノであるという点においては両者の間に相は入らない。すなわち、今日の数学的存在の世界観は物理的存在の世界観とは相容れない(一致しない)。カントールが無限を数える方法を発見したのはフーリエ級数表現の一意性に関する研究を通じてであった。
{\displaystyle {\begin{aligned}a_{n}&={1 \over \pi }\int _{-\pi }^{\pi }f\left(t\right)\cos nt\,dt,\left(n=0,1,2,3,\cdots \right)\\b_{n}&={1 \over \pi }\int _{-\pi }^{\pi }f\left(t\right)\sin nt\,dt,\left(n=1,2,3,\cdots \right)\end{aligned}}}
(メモ)同じか同じでないかということははなはだあいまいな概念であり、見る者の世界観にも大いに依存する。リンゴとバナナは味も異なるし、値段も異なる。しかし、抽象化の階段を昇(のぼ)って果物、さらには食べ物というメタ的な観点に立てば両者の間に相は入らない。一般に空間の形とか空間の形態とかいうものは一言で片付くほど単純・明解なものではない。具体(ぐたい)・抽象(ちゅうしょう)・組み合わせの階段が入り乱れてこの観点に立てば相は入らないが、この観点に立てば相が入るということが実に多いのである。これに関してより詳細を知るためには位相空間の理論について学ぶ必要がある。すなわち、新聞紙に正円(せいえん)を書いて、それが書かれた新聞紙をクシャクシャに丸めてからふたたび広げたものであってもそこにかかれている円を、やはり同じ円の仲間であると捉える世界観である!
(参考文献)
都筑卓司、トポロジー入門、講談社.
(例)カントはユークリッド幾何学を必然的(essential)かつ普遍的(universal)なものであると考えた。いまでは、数学の世界においてさえも、ユークリッド幾何学が統一(合)的なものでも、普遍的なものでもないことをわれわれは知っている(ユークリッド幾何学における平行線の公理は他の公理とは独立な公理であり、これに修正を加えることによって楕円幾何学や双曲幾何学など、多様性に富んだ非ユークリッド幾何学の豊かな世界(鉱床・鉱脈)がユークリッド幾何学とともに数学の世界において(相)並立(あいへいりつ)・(相)並存(あいへいぞん)しうるということをわれわれは知っている!※)。実際の物理空間がユークリッド幾何学に従っていないことは観測によって実験(経験)的にも確かめられている。
※リーマンは局所的にユークリッド幾何学、楕円幾何学、双曲幾何学のいずれかが成立する空間をパッチワークのようにつなぎ合わせることで、空間を構成しようと考えた。この考え方はアインシュタインの相対性理論およびこれにもとづくわれわれの住むこの(宇宙)空間の形状の理解・解明へとつながる重要なコミュニケーション・リンク(およびそこで働く超偉大なるテンション(超万有引力!))を有している。
しかしながら他方(たほう)で、閉曲線と正円(せいえん)、開曲線と直線の関係よろしく、非ユークリッド幾何学を理解するためにまずは、すべての幾何学の基礎・基盤・土台・土俵・インフラストラクチャたるユークリッド幾何学を標準型(ひょうじゅんけい)としてイメージすることはとてもとても、本質的にきわめて重要であり、われわれ人類が、延々・脈々・累々と(ぐるぐる巻きに!)ユークリッド幾何学を学んだり、研究してきたことには大きな意義がある!※
※射影幾何学(しゃえいきかがく)上の問題をハンドリングする際にも同様にまずは、その特別な場合(キャプテン、花形選手)である3つの基底(座標軸)が直交する正規直交基底上で展開されるユークリッド幾何学において対応する問題がどうであるかについて考え、つぎに基底(座標軸)の交わる角度や目盛りの条件を緩(ゆる)めてすこしづつ変化・変容させてみたときに対応する問題がどう変化・変容するか(あるいはしないのか)について考えるのが直観的で見通しの良いハンドリングにつながるだろう。
なぜなら、たとえ曲がった曲面(多様体)であっても、面上の各点ごとに接ベクトル空間としてのユークリッド空間(チャート)を(イデア論的な1次線形近似)モデルとして導入することができる。そうして正規直交基底を土俵とする線形なユークリッド幾何学は計量性の面で優れており(内積や距離・角度が定義でき)、直観的(幾何学的、野性的)にきわめて見通しが良く単純・明快であり、だれもが簡便かつ随意に、安全・安心・安定的に( Me-DigIT 魂のこもった!)思いやりをもってハンドリングすることができるものだからだ。
ためしに手元にある新聞紙に定規で直線を引き(ハンドリングしやすい正規直交基底(せいきちょっこうきてい)のユークリッド幾何学の世界でまずは扱い)、つぎにクシャクシャに丸めて(基底の直交性などの条件を柔軟(Topological)にゆるめて)、もう一度広げてみよう(あるいは、ゴム膜に直線を引いて、ゴム膜上にゴム紐を通してあっちこっち引っ張ってみても良い)。非ユークリッド空間の土台としてのユークリッド空間の重要性が体感できるであろう。
たとえ曲げられた空間であっても(その源泉(げんせん)として対応する標準型としてのユークリッド空間上を)真っ直ぐ進むことが可能である(原始的な解は抽象化の階段を1段のぼった(上流にある、あつかいやすく典型的な源泉(げんせん)にある)空間で得て、さらにはそれをもとに川下(かわしも)へと順々に下りながら辿(たど)り、個別具体的な(実装)解を導出したとしても一向に構わないのである)!(これは人生を歩むうえでも示唆(しさ)に富む事実である)
(例)ガウス・ボンネの定理の証明にとって必須であるストークスの定理は、まずはユークリッド平面という平(たい)らかな空間でその議論を行ない、つぎにこれを多様体上へと拡張・展開する道順を順々に辿(たど)るほうが直観・幾何学・野性的に見通しよく単純・明解に理解することができる。
医療専門家(プロ)は血管(尿管、腸管など)を曲線(管)状構造体として、腫瘍(や結節、結石など)を球状構造体として普遍・一般・抽象化したメタ的なモノとして捉えているのだそうだ(したがって腎臓や肝臓も球状構造体と捉えられる)。この方法は、テーラー展開の1次線形近似的な捉え方であり、実際の腫瘍や臓器は完全な球ではないが、プラトンのイデア論よろしく位相(柔軟な)幾何学的な球と捉えることは統一・統合・普遍的で直観的(幾何学的、野性的)に見通しよく単純・明快で、なおかつきわめて合理的である!
(例)本質的な部分を抽象化して観れば、人間は一見、球と同相のように見える。しかしながら、人間の消化器系までを考慮に入れるとトーラス(ドーナツ)と同相であるかのように思える。消化管の中は(なんと!)体の内側ではなく、外側であったのだ!さらには、喉(のど)のところで鼻の穴と口とが分岐しているのだから2-トーラス、あるいは鼻の穴の数までを考慮に入れれば3-トーラスと同相だと考えることもできよう。また、一般の血管系は穴の数がn個のn-トーラス(n-ジーナス:n人用の浮き輪)と捉えることもできるだろう。
(例)線分の両端を無限の彼方(かなた)まで伸ばした直線(あるいは開曲線)は、その両端が無限の彼方でつながっている(すなわち曲率半径∞の円弧)と捉える世界観においては、正円(あるいは閉曲線)と一対一の対応がついてしまう。すなわちこのような世界観のもとでは(なんと!)正円(あるいは閉曲線)と直線(あるいは開曲線)の間に相は入らない(区別がつかなくなってしまう)。
これについてより詳細を知るためには、角度を保存しながら直線/正円を直線/正円に写す共形(あるいはその二つ名を等角ともいう)写像の理論やn次元双曲幾何学のモデルであり、その幾何学のもとでの各点が n次元円板あるいは球体に属し、かつその幾何学のもとでの直線がその円板に含まれる円板の境界と直交する円弧または直径によって与えられる有名なポアンカレの円板について学ぶ必要がある。
(参考文献) 富岡礼子,曲がった空間の幾何学,講談社.
(例)『ものさし』が異なれば、円(球)の形状もさまざまに変わる。ユークリッド距離(ユークリッド幾何学)では円(球)は通常われわれがイメージする円(球)であるが、距離の定義が異なれば、ひし形(正八面体、絶対値|x|+|y|(+|z|)=r)や正方形(立方体、max(|x|,|y|(,|z|))=r)にもなりうる。
位相(柔軟な)幾何学ではこれらの多様な円の間に相を入れない(同一視する)。これに関連して超楕円(superellipse)という概念がある。超楕円は臓器の輪郭のフィッティングに応用されるなど、医用画像処理においてもきわめて有用な関数である。
(例)実に驚くべきことでにわかに信じがたいことだが、如何なる2次曲線(楕円も放物線も双曲線)も観方を変えて、ある視点(2次曲線がその側面に包含される円錐の頂点!)から観てみれば(なんと!)すべて円に見えるという(これらの2次曲線がその二つ名を円錐曲線と呼ばれるゆえんである!)。そうしてあらゆる2次曲線は円とある種の性質を共有する。たとえばパスカルの定理は円だけでなく、どんな2次曲線においても成立している。これに関してより詳細を知りたければ平行線を平行線に写すことをその特徴とする射影(しゃえい)幾何学について学ぶと良い。
xy平面上の点(x,y)の軌道が線形微分方程式で与えられているとする。この点と原点を通る直線の勾配z=y/xは有名なRiccatiの方程式で支配される。
これはマシンビジョンの理論とも関連している。すなわち、原点にカメラを置けば、原点を通る同一勾配の直線上の点はすべて同じ点に投影(縮退)され、同じ点として(縮退して)観測されてしまう。Goshらはこれを拡張して透視システム理論(perspective theory)を展開し、物体運動の同定可能性や観測可能性についてRiccatiの方程式に基づいて論じている。
真正面からまっすぐ近づいてくる相手との距離感はきわめて測(はか)りづらい。どんなに相手が強くても真正面からぶつかる戦法がきわめて有効に機能するゆえんである。超音波画像においてもこれは同様であり、(3次元空間のうち、縮退していない)面内の物体運動は同定しやすいが、面外の(奥行方向の)物体運動は(超音波画像上で縮退しているがために)きわめて同定しづらい。
具体的に超音波医用画像においては、視野(超音波プローブの視線、スキャン面、視野角)が3次元ユークリッド空間内に埋め込まれた2次元ユークリッド面内で扇(おうぎ)状に縮退・制限されている。このため、プローブのスキャン面内の物体運動については捉えやすいが、面外の物体運動については捉えにくい。
また、深度においても深部になるほどノイズや解像度が低下するため、物体運動が捉えずらくなる。さらに超音波ビーム・フォーミングの際のフォーカス・ポイント設定についても考慮が必要である。すなわち、超音波スキャン面内で(超音波画像中央付近に)ゴールデン・ストライク・ゾーンが存在することになり、そのなかに観察対象物を画像のブレやノイズを極力抑えた状態で捉える必要がある。
(参考文献)
玉野研一,なっとくする無限の話,講談社, 2004.
狩野弘之, 西村敏充, Riccati方程式と制御問題, J.SICE, Vol.35, No.5, 1996.
(例)線形性は一般の関数(写像)を(局所的に)1次近似することによって得られる初等的な性質だが、『原料を2倍にすれば、生成物も2倍になる』など、直観(幾何学・野性)的に関数(写像)の増減傾向を把握できるため、(特にわれわれ人間にとっては!)きわめて有用な性質である。(偏)微分(差分)操作によってだれもが簡便に得られる。ゴム膜に書かれた(柔軟な幾何学上の)直線よろしく、現実世界が非線形であるからこそ、理想的(イデア)なモデルとしての線形(性)を想起することが尊(とうと)いといえる。
(例)現実世界が非対称であるからこそ、理想的(イデア)なモデルとしての対称(性)を想起することが尊い
(例)機械製図におけるセオリーのひとつに、『カクカクしたものの対称線はできるだけ省略できないか検討する』というものがある。これは機械製図において対称線を引く際には、『指定した寸法精度で対称性を管理してくださいね!』という加工業者にあてた主張(メッセージ)であると受け取られてしまう可能性があるためである。このため、本来そこまでの対称性が精度的に必要なかったにもかかわらず、余計な精度管理の工程やこれにともなうコストが発生してしまう。
『機械製図は(加工業者との)コミュニケーション』と言われるがやはり、余計な一言はなるべく言わない方が吉である!他方で、ドリルや旋盤などで円筒形の穴をあけるときの中心(軸)線は基本的に省略しないのが通常である。さらにはまた、要領を得ず、直観的にわかりにくい図面もまた、加工業者が部品の構造を理解するために時間を要するため、コストが高くつく傾向にあるそうである(加工業者やはり、感情をもつ生き物である!)。直観的に見通しのよい、理解しやすい図面は、ただそれだけでコストパフォーマンスの面で優れており、加工業者にとって、ごちゃごちゃしていない、わかりやすい図面を書ける人は職場で重宝(ちょうほう)されることになる。
(例)現実世界が非剛体であるからこそ、理想的(イデア)なモデルとしての剛体(性)を想起することが尊い
(例)ある理論に矛盾がないことを主張するための有効な手法のひとつとしてその理論と機能面で等価なモデル(模型・おもちゃ)をまずは試作してみる方法がある(まずは機能試作法)。もし、その理論から矛盾が導かれるようであれば、試作したモデルにおいてもやはり、同様の矛盾が導かれるべきであろう。そうしてそのような矛盾があっては、試作したモデルと機能面で等価なもとの理論(これも実はひとつのモデルである!)の有効性(無矛盾性)を主張することはできないからである。
(参考文献)
イアン・スチュアート,川辺治之訳,無限,岩波科学ライブラリー,2018.
玉野研一,なっとくする無限の話,講談社,2004.
(例)(一般および特殊)相対論などは物理学の問題でありながら人間の直観が及びにくく、超感覚的であるという意味で高度に数学(創造)的でもあり、時と場合によって直観は有害にすらなりうる。
相対論では4次元を扱っているが、第4番目の座標はあくまで時間であり、宇宙空間自体としては3次元を扱う。ただし、この空間は3次元のユークリッド空間ではなくて重力場の理論により、蒟蒻(こんにゃく)よろしくグニャリと曲げられているところがユニークである。
静電磁場ではマクスウェル方程式は別々の対(つい)に分かれ、一方の片割れは電界、他方の片割れは磁界で両者の間には一見したところ、コミュニケーション・リンク(およびそこで働く超偉大なるテンション(超万有引力!))など何も存在しないかのようにおもえるが、電界(場)と磁界(場)とは本質的には(なんと!)同じものだったのであり、磁界は電界の相対論的効果としてこれらを統一・統合・普遍的に抽象化してメタ的にハンドリングすることができるという、(特殊および一般)相対性原理に基づく強固な結びつきが存在する。この(特殊および一般)相対性原理はマクスウェル方程式の発見後にアインシュタインによって見出された。
当時、アンリ・ポアンカレ(数学者)は如何なる慣性運動する座標系においても光の速さは一定(~30万km/s)でなければならないという条件(光速度不変の原理)を導き出すところまではできていたのだが、まさか現実の物理世界が蒟蒻(こんにゃく)よろしくグニャリと曲げられており、この条件に従っているというところまでは物理的世界観として十分に咀嚼(そしゃく)しきれてはいなかった。
他方アインシュタイン(物理学者)は(超!?)直観(幾何学、野性)的信念のもとにこの条件を物理的世界観として蒟蒻(こんにゃく)よろしくグニャリと柔軟(!)に受け入れることができ、1905年に特殊相対論(独: Spezielle Relativitätstheorie、英: Special relativity)として発表した。
そのなかでアインシュタインは光速で伝わる重力波の存在を予想している。電磁波が光速で伝わることはマクスウェル方程式が教えてくれるが、重力波もまた、光速という有限の速度でこの宇宙を駆け抜け、徐々(じょじょ)に伝播(でんぱ)してゆくと言うのである。
そうしてアインシュタインの死後、半世紀以上の時が経ち2015年9月14日9時51分 (UTC:協定世界時) にLIGO(ライゴ、Laser Interferometer Gravitational-Wave Observatory)実験によって実際に重力波の存在が確認されることとなる。
この重力波は地球から13億光年離れた2個のブラックホール(それぞれ太陽質量の36倍と29倍)同士の衝突による融合合体(fusion)によって生じたものであるという。まさに『ドラゴンボールの世界観』である、、、
(参考文献)
都筑卓司,トポロジー入門,講談社.
~~~~~~~(知性・知能とのコミュニケーション・リンク生成による野性・野能の変化・変容・洗練・進化法)
(人生の理念・心意気)
雲外蒼天(うんがいそうてん)の心持(こころも)ちであきらめることをあきらめる!→人生の辞書から失敗(試合終了)という概念をなくす。あるいは、時間的(歴史観)・空間的(世界観)・人-物間(じんぶつかん:人-物観・人生観・哲学・動力学はじめ、あらゆる自然科学)的に拡げてみた場合、失敗経験を積むことは成功につながる、真(しん)に頑健(がんけん)な手法(あるいはシステム)を構築/産生(さんせい)するうえで必要不可欠なものであり、なおかつ本質的に(intrinsically)重要なプロセスの一部を構成しうるものだと考えることにする(
成功へとつながる『真の頑健性』は失敗からの復活体験によってこそ生まれるのだ!失敗は結果としてではなく、成功へと至る頑健なプロセスの一部を構成する重要な要素なのだとして想像力逞しく捉えよう!これにより、『失敗経験はかけがえのないすばらしい宝』ともなりうるのだ!)。すなわち、いろいろと何度もトライしてみた結果としての失敗経験を(ぐるぐる巻きに!)積み重ね、その中から失敗のメカニズムをうまく抽出してこれを分解・再構築して(ぐるぐる巻きに!)再度トライする真に頑健な姿勢(
Rolling Me-DigIT ! の精神)こそが決定的に重要になってくると言うのだ!
旅に終わりがあることは素晴らしい。でも、もっと重要なのは旅そのものなのだ。(Ernest Miller Hemingway)
遠回り(や寄り道)をするからこそ、見られる景色(絶景)がある!
見知らぬ街で道を間違えることで、たまたま見つかる穴場スポットとの出会いもある!これによりその街のことがより好きにもなり、またより詳しくもなれる!これと同様に、あるとき見知らぬ研究分野のあるところで問題に突き当たって、そこで試行錯誤を繰り返しながら失敗(エラー)経験を積む中で(ぐるぐる巻きに!)蓄積される数々の知見(
Get the Rolling Me-DigIT HARVEST!)が実はわれわれの血肉(けつにく)となる宝であり、別の問題を解くときにも生きてくる。
江戸の仇(かたき)が長崎で討たれたり、あるいは時空を超えて今日(こんにち)の東京で討たれたりすることも十分に起こりうるのである!
虚数iは決して想像上の架空の(imaginaryな)ものなどではなく、2次以上の方程式の根を統一・統合・普遍的に構成するうえで不可欠なこの世界にも(少なくとも世界観モデルとしては概念(イデア)レベルで)実在するきわめて実用的な数として捉えるべきものであろう(ここで、虚数iが実際にこの世界に(物理的に)存在するかどうかを考えることはさして重要ではない(すくなくとも数学的な世界観モデルとしては概念(イデア)レベルでこの世の中に実在している!と言い切れる。数学的な対象は概念的なレベルにおいて(のみ)現実である!)。そのような世界観(モデル)をまずは持ってみてあれこれと推論を展開してみることこそが有効で、本質的かつ決定的に重要なのである!)。複素数はひとつの数の内に複数(対となる2つ)の要素としての実数(代数幾何学的には平面上の点)を内包する。
これにより物事を統一・統合・普遍的で直観(幾何学・野性)的に見通し良く、だれもが簡便に表現しうるのである。複素数の入出力をハンドリングしうる複素関数論はきわめて実用的であり、電磁気学はじめ、超音波工学、ロボット(制御)工学の分野においても大活躍している。
(例)われわれが日常的に用いる『姿勢(軌道)』という概念はすべて球面(上の点の軌道)という幾何学的な世界観で統一・統合・普遍的かつ直観的に捉えることができる。ロボットの剛体姿勢(軌道)はオイラー・パラメータと呼ばれる4元数(クオータニオン)を用いて、4つのパラメータで表現可能である(ただし、ロボットの剛体姿勢とクオータニオンが1:2の対応関係になっていることには留意が必要である)。
オイラーパラメータの特長として特異点が存在しないため、ロボティクスのみならず、ロケットや人工衛星の姿勢制御などに幅広く応用展開されている。剛体姿勢(SO(3):正規直交群:回転(運動)群)のつくる軌道はオイラーパラメータや単位クオータニオンによってS^3(3次元球面)へと写像される。
クオータニオンは複素数の(一般のn次元への)拡張である超複素数として1843年10月16日、ハミルトンがダブリンの街を運河に沿って歩いているときに発見したといわれている。発見当時、ハミルトンは3次元への複素数(2元数)の拡張を研究しており、その結果として4次元への複素数拡張を見出したのだという。
具体的にクオータニオンの式はかの有名なオイラーの恒等式(2次元の姿勢変換を表せる2元数)の4元数拡張(3次元の姿勢変換を表せる)になっている。ここで、nは回転軸方向の単位ベクトル、ψは回転角を表す。いかなる複雑な剛体の姿勢変換も一つの回転軸ベクトルとそのまわりの1回の回転で表現できる※ということは実に驚くべき重要な事実であるが、クオータニオンの式はこの事実を直観的かつ明解に体現している(まさに率直な数学的表現が物理の本質を垣間見せる好例と言えよう!)。
※これは(なんと!)一般の(n+1次元ユークリッド(運動)空間に埋め込まれた)n次元超球面でその(運動)軌道空間があらわされる回転(運動)群(SO(n+1))においても成り立つという※※。具体的にn次元超球面(運動軌道空間)上の任意の2点p,qを適当に選べば、原点を含めた3点で定まる(n+1次元ユークリッド(運動)空間に埋め込まれた)2次元平面内の原点を中心とする1回の回転(運動)群(SO(2)⊂SO(n+1))によってpをqに写すことができる。これに関して詳細を知るためにはリー群の表現論についてさらにより深く学ぶ必要がある。
※※n+1次元ユークリッド空間に回転(運動)群(SO(n+1))が作用すると、(n+1次元ユークリッド(運動)空間に埋め込まれた)n次元超球面というあらたな(運動)軌道空間が生まれる。
超複素数には他にもオクタニオンとよばれる8次元への拡張が存在するが、これら4および8次元のみに限られていることは興味深い。このことは(超)外積という演算の存在が3次元および7次元のみに限られていることと双対(そうつい/そうたい)の関係にある((超)外積の3次元および7次元は虚軸の数(次元)に対応しており、これに実軸の1次元を加えればそれぞれ4次元および8次元となり、クオータニオンおよびオクタニオンの次元と一致する)。
(参考文献)
[1] 内山 勝, 中村仁彦, ロボットモーション, 岩波書店, 2004.
(例)2次元翼の理論においては、まずは単純な形状である円柱まわりの流れを複素数を用いて表現し、つぎに複素平面上の円をジューコフスキー変換すると翼形状になることを利用して複雑な形状である翼まわりの流れを同定、これにより複素トポロジー解析的に翼に働く揚力をシミュレーションするという2段階戦法を採用している。
(例)動力学において物体が回転運動する状態を回転軸方向の1個のベクトルできわめて簡潔に表現する際に用いる角運動量ベクトルL=r×pも虚数iと同様、実際にそのようなベクトルがこの世界に存在するかどうかを考えることはさして重要ではない(すくなくとも物理的な世界観モデルとしては概念(イデア)レベルでこの世の中に実在している!と言い切れる)。そのような世界観(モデル)をまずは持ってみてあれこれと推論を展開してみることこそが有効で、本質的かつ決定的に重要なのである!角運動量ベクトルを運動量ベクトルとのアナロジー(analogy、類似性)で捉えれば、並進および回転運動を統一・統合的かつ直観・幾何学的にハンドリングできる。
試行錯誤(Trial and Error)の過程は泥臭くて通常、問題集の解答例にはのっていないものである(解答のエレガントさを優先する過程で直観(幾何学、野性)的な単純・明解さ、すなわちアフォーダンスが低下する)。
他人とのディスカッションの過程においてはその目的・力点を相手のモノの見方・考え方・捉え方・発想の仕方・世界観(軸)を推察、これを学び、そのモデルを構築すること(世界観(軸)学習)にこそ置くべきである。このとき、自身の世界観(軸)と相異なる世界観(軸)の存在を知ってしまった場合(これは多様性の観点からも、とても重要な知見になりうる!)にもあわてて反論する必要など全くなく、『わかるわかる!そういう(あなた方の)世界観(軸)も(われわれの世界観(軸)が存在しうるのと同様に)存在しうるよね!』の精神で、一定の共感を示しながら柔軟にその世界観(軸)の存在をまずは認めて相(あい)並存させる方向で対応しておくことが余計な摩擦を生じさせないうえで好適である(全く相異なる世界観(軸)で直交補空間の関係にあったとしても多様性の観点から、並存させておいて一向に構わないのである!そうしてそれら相並存する世界観(軸)どうしはお互いにモーメントを掛け合う関係になれるのである!法)。
(例)ユークリッド幾何学(の世界観(軸))と楕円幾何学、双曲幾何学をはじめとする非ユークリッド幾何学(の世界観(軸))とは相並存しうる。そうしてそれらは直交補空間の関係にある。
(例)連続体仮説が成り立つ世界(観(軸))と成り立たない世界(観(軸))とは相並存しうる。そうしてそれらは直交補空間の関係にある。
(例)選択公理が成り立つ世界(観(軸))と成り立たない世界(観(軸))とは相並存しうる。そうしてそれらは直交補空間(平行世界ともいえる)の関係にある。
(例)n次元固有(関数)ベクトル空間とm次元固有(関数)ベクトル空間のそれぞれの基底(関数)ベクトル同士の合計n×m組のモーメントや内積をまずは考慮すればよい。
(例)方程式のゼロ点(解)はひとつとは限らないし、線形空間におけるゼロ空間(解空間)はひとつの基底から構成されるとも限らない。思いもよらない別解が存在しうる可能性は常に意識しておくべきことであろう。われわれひとりひとりが空間内の点で、空間がわれわれの住み処(『社会(宇宙)』)であるとするならば、複数の基底から構成される、世界(価値)観の多様性を許容する、自由度が高い多次元空間としての『世界』のほうが、住み処(『社会(宇宙)』)として優れているのではなかろうか(すくなくとも私はそのような『社会(宇宙)』に住みたい)。
なぜならそのような『社会(住み処、宇宙)』には、包容力があり、窮屈でなく、そしてなによりもVarietyがあって退屈しないからだ(そこでは、複数の世界(価値)観が共存しうることに着目されたい。相手の世界観を頭ごなしに否定する社会(住み処、宇宙)になることだけは何としても避けたいものである)。冗長空間(ゼロ空間)は居住性においてとても重要な役割を果たしていると言えるのだ!
(例)線形微分方程式系で頻回(ひんかい)に行なう、exp X の計算は基底座標系の再設定(取り替え)により、Xを対角形あるいはジョルダン標準形で再表現しなおしたうえで行う方が直観・幾何学・野性的に見通しよく単純・明解である。
(例)行列Aが対角化できるかどうかの必要十分条件は、
(固有値の重複度)=(固有ベクトル空間の次元)
が行列Aのすべての固有値に対して成り立つことである。すなわち、(一見したところ冗長にも思える)同じ固有値を有するもの(重解の片割れ)どうしであったとしても複数の世界(価値)観が固有ベクトル(軸・柱・はり)としてわれわれの社会(住み処、宇宙)に存在していることには(その固有ベクトル空間(小社会、小宇宙)の居住性をしっかりとしたものにするうえで)大いに価値がある!
(例)同相(どうそう)とは互いを他に写しあう連続写像が存在するということである。連続写像とはつながっているものをつながっているものに写す写像のことである(つながっているのか?いないのか?それが本質的に重要だ!)。互いを他に写しあうためには、写像する際にその片割れがつぶれてしまったりするようでは(点と点との1対1対応という観点から)困るので、双方の空間が縮退(しゅくたい)せずに次元の広がりを(その空間の構造として)保つ必要がある。
まずは、起点・原点・出発点(starting point)・一丁目一番地と最終目的地といった初期条件や境界条件を明確にする。つぎにその間を埋めるべき基礎・基盤・土台・根本・布石・伏線といった土俵設定、根幹枝葉花(果)実、目標・目的・マイルストーン・最終目的地・中継地といった本質のつながりを探る。
科学のどの進歩にも完璧な無知からはじまって、証拠にもとづく部分的な知識が(超万有引力!的につながって)しだいに確実になるという段階を経て、事実上確実になるという段階に至るという(複利的)変遷が含まれる(Howie)。
最適な『道(どう)』を知るためにはまず、その周辺にある『多様な道(の構造!)』や、さらにはその対極に相当する『(双対・相補的な)道(の構造!)』を知っておくことこそが効果的である。なぜなら学習に寄与する有用で良質なフィードバックが得られるのは周辺の多様な道や対極に相当する道を多様に歩いた場合であるからだ。これはcos関数とsin関数とが位相的に観て双対・相補的な関係にある(複素平面上の点を極座標で表現することを考えてみよ!)ことと類似的(similar, analogous)である。『○○道』は実に多様で奥が深いのだ!
(例)鞍点(あんてん、saddle point)は見る方向(世界観)によって山にもなるし、(90度視点を回転すれば)谷にもなっている(メビウスの輪よろしく手近にあるベルトをひとひねりして巻いてみても鞍点の地形があらわれる)。これもまた、cos関数とsin関数とが位相的に観て双対・相補的な関係にあることと類似的(similar, analogous)である。鞍点は2次元球面(われわれにとっては通常の球面)の表と裏を(自己交差を許容するという条件のもとで)ひっくり返すうえでも本質的に重要な幾何学的構造である!2次元球面とは異なり、鞍点を幾何学的構造としてつくれない1次元球面においては(それが包含される2次元平面内の操作で)表と裏をひっくり返すことはいくら悔しがったところでできないのだ(この事実はまさに、次元のもつ破壊力を我々にまざまざと見せつけるものである)。
ここで1次元球面(われわれにとっては通常の円周)では現れなかった鞍点が高次元球である2次元球面では山と谷に加えて地形のvariety(多様性)として新たに生じていることに着目されたい。この鞍点の存在が自己交差を許せば位相幾何学的(連続的かつなめらか)な変形のもと2次元球面の表と裏を(それが包含される3次元空間内の操作で)ひっくり返すうえで本質的かつ決定的に重要な役割を果たすのである。そうしてこの2次元球面の表裏をひっくり返す操作は
バナッハ・タルスキーのパラドックスにおいて自己交差を許して、1つの球を2つに分割する操作と類似(Analogous)である。
ピンチはチャンス!鞍点を見極め、ここぞというところで運動軌道に(奇跡を起こすための伏線としての)特異点をつくり、(90度(柔道の場合は180度))切り返して思いきって『一撃必殺の返し技』を打とう!他方、相手にとっては『一撃必殺の返し技』を打とうとするその気概そのものが脅威となり、うかつには踏み込めないだろう。すなわち鞍点では地政学(ちせいがく)的な条件にもとづく精神・心理的な均衡(きんこう)状態が巧妙に醸成(じょうせい)されていることになる。
負けの9割は相手と戦う前に自分自身にすでに負けているのだという。人生は大いなる精神・心理戦である。これについてよく知るためには、ラプラス演算子やこれによって表される調和関数(勾配流の出入りの収支がいたるところ±0)など、勾配(ベクトル場)流の理論についてさらに深く学ぶ必要がある。(鞍点は『一撃必殺の返し技』を打つビッグチャンス法)
(例)実際の医療診断や手術では物理的に実現できないような芸当(げいとう)もデジタル空間上での3D臓器のシミュレーションであれば自由自在で可能である!具体的にたとえば、
『Outside in』よろしく、実世界では不可能な自己交差を許すことで臓器の表と裏をひっくり返して観察するような操作すら可能である。このように、医療・バイオ・福祉の世界はデジタル(な機能関数群:医デジ化機能関数群)によってどんどんと、とことんまで拡大することができるのだ(Me-DigITプロジェクトのコア・モチベーションかつコア・コンセプト)!
(例)素人は特異点を扱いが困難で得体の知れないものとして、忌避(きひ)しがちな傾向にあるが、『虎穴に入らずんば虎子を得ず』のことわざよろしく、(数学の)プロは扱いが困難で得体の知れない特異点の付近でこそむしろ、なにがしか重要な手がかりが隠れていやしないかと刮目(かつもく)してよくよく調べようとするのだという(これまた偉大な精神・心理戦である)。
ここでわれわれが言うところの( Me-DigIT ! )超特異点とは、特異点の一般化(ここではまずは、さまざまな分野で使われている特異点という用語の成立要件をあえてゆるめて広義かつ超超越的に捉えてみよう!※)であり、(地形的に見て)周囲(の環境)とは一線(いっせん)を画(かく)しており際(きわ)立って(突出して、卓越して、とんがって、(ゲゲゲの鬼太郎よろしく!)髭のような(不気味でなにやら)得体(えたい)の知れないものなんかまで生(は)えていたりなんかもして)様子・様相(ようそう)が大きく異なり(変化しており)、『(たとえば×点などを打つなどして)シンボル化』される(できる)ようなところ((宝の!)地図でいうところのシンボル化された記号が打たれているような点)といったくらいの意味合いである。
(例)医用画像上でいうと臓器やこれに包まれた腫瘍( tumor )や結石( stone )などの病変部( focal lesion )等
(例)人の顔でいうと目・鼻・口等
※すなわち、普遍・一般・抽象化してメタ的に捉えなおしてみよう!
(例)新幹線の秋田駅から次の停車駅の大曲(おおまがり)駅までの約30分間、こまちは逆走状態となる。これは、秋田ー大曲間の奥羽本線とその後の田沢湖線の配線がアルファベットの「r」の様にスイッチバックで接続されているためである。また、この「r」型のスイッチバック(特異点)による切り返しが秋田新幹線の旅の魅力(charm point)として秋田県の見逃せない名所のひとつになっている。地勢(ちせい)を見極め、ここぞというところに誘い込んであえて特異点(ひっかかりポイント、マーカ、アトラクタ)をつくり、180度切り返して思いきって打たれた『一撃必殺の返し技』の好例と言えよう。
電気通信大学の最寄り駅である調布駅(
副駅名標:電気通信大 最寄り駅)もまた(超)特異点にあたり、京王(けいおう)線と京王相模原(さがみはら)線の分岐(ぶんし)駅であり、その配線がアルファベットの「て」の形になっている(親しみを込めて『
てつみち』と呼ばれている)。調布駅はまた『映画のまち』の駅としても知られ、1日の平均乗降人員は約10万人である。この数は京王電鉄の駅のなかでは新宿駅、渋谷駅、吉祥寺駅(いずれもターミナル駅)についで4番目に多く、京王電鉄単独の中間駅としては最多となっている。
(例)投打の二刀流で有名な大谷翔平選手は、スライダーに加えて、当初はスライダーと同じ軌道ながら途中で分岐(ぶんし)して反対方向に曲がる運動軌道をもつシンカーを使う。スライダーのみだと、打者は『踏み込んで打つ』などの対策がとれるが、シンカーという分岐線(ぶんしせん)があるかと思うとうかつには踏み込んで打つことができない。ビュリダンのロバではないが、スライダーにシンカーという分枝線を加えることによって意思決定の問題が打者にズシンと重くのしかかる(これまた偉大な精神・心理戦である)。そうして、意思決定におけるコンマ何秒かの気の迷いはバットの振りの鋭さ(キレ)を数センチあるいは数ミリの精度で鈍らせて(運動ポテンシャルエネルギーをわずかに減退させて)打者の自滅(じめつ)を誘(さそ)うことになる、、、スポーツはじめ、負けの90パーセントは自滅にあることに留意されたい。
オイラーの公式
特に、θ = π のとき

となり、この関係はオイラーの恒等式(Euler's identity)と呼ばれる。
そうして起点・原点・出発点・starting point・一丁目一番地たる初期条件は一般にさまざまであることを忘れてはならない!カードが配られた瞬間に最終目的地(終端条件)に位置するロイヤル・ストレート・フラッシュが揃っている幸運なケースは確率的にみても稀であろう、、、
(例)DNAの二重螺旋(らせん、double helix)構造はcos関数とsin関数で表現され、双対・相補的な(幾何学的構造)関係にあるがために損傷に強く(頑健、ロバストである!)、複製の際にもコピーミスが起きにくい。
(例)電磁波は池に小石を投げ落としたときに生じる波紋(はもん)のごとく、光速という有限の速度で宇宙空間を徐々(じょじょ)に伝播(でんぱ)してゆく。具体的に、電界が磁界を誘導し、磁界が電界を誘導するといった具合に電界と磁界は対(つい)になって相互作用しながら、90度位相のずれたsin波、cos波としてチェーン状に伝わってゆく。医療分野で応用されているX線(CT)やガンマ線(重粒子線治療)なども電磁波の一種である。電磁波は計測においてはノイズの原因としても知られ、医用画像上に顕(あらわ)れる場合にはシールドを施すなどの対策が必要になる。
(cos(t),sin(t),vt/2π)と(-cos(t),-sin(t),vt/2π)の対はz軸を軸として一回転する間にv進む、位相(t)がπだけずれた(実際のDNAの場合にはこの位相差はπより小さいらしい、、、)二重螺旋構造になっている。これを回転運動(cos(t),sin(t),0)と等速直線運動(0,0,vt/2π)の線形和として捉えれば、直観(幾何学、野性)的にも見通し良く、単純・明解で簡便にハンドリングできる。
他方、RNAは1本鎖であるがために2本鎖のDNAの場合とは異なり、複製の際にコピーミスが生じやすい。このためCovid-19など、RNA型のウイルスには変異型が多く、治療時の対応をより困難なものにしている。
これに対して治療薬開発の現場では、RNAのコピーを阻害するための薬を複数まぜて同時に使用するという対応策が用いられている。RNAのコピーの際に複数箇所が同時に変異する確率は十分に小さいため(why 微小な確率の積)、この方法はRNAのコピーの阻害において有効に機能してウイルスの増殖を抑制できることが知られている。
すなわち、(世界観)学習に寄与する有用な良質のフィードバック(鍛錬・洗練)を得ることを目的とする経験値(知)獲得論的な観点に立てば、最適な道はかならずしも最良のフィードバック(鍛錬・洗練)を与えてくれる、言わば『知的な』最適解とは到底言えない(位相的に観て最適解から適度にずれやゆらぎがある、言わば『付かず離れず』の多様な道をあえて選択してあえて適量の(Errorをともなう)失敗経験を積み重ねながら歩むようにしたほうが(人生を全うするための固有(関数)ベクトル空間の成長にとっても)有用な鍛錬・洗練が得られて(世界観)学習にとってはむしろ良い)のだ!ひとつひとつ異なる、多様な旅の(失敗)経験値(および経験を蓄積するプロセス)に(よる人生を全うするための固有(関数)ベクトル空間の拡張に)こそ我々は価値を置くべきである!
研究の有用性の主張には2つの方法がある。
ひとつ目は、提案手法(条件)によりこれまでで最上のパフォーマンスが出ることを実証すること
二つ目は、うまくゆかない方法(環境条件)とすこしでも性能が改善した方法(環境条件)とを比較し、なぜ改善したのか、その機序(きじょ)・構造を説明する理論体系を構築すること
ひとつ目のほうが一般に華々(はなばな)しく、周囲から注目もされがちであるが、じつは二つ目の機序・構造論研究(いろいろと何でもトライしてみて失敗のメカニズムを抽出してこれを分解・再構築できること!)にこそ研究における本質的な価値がある!と捉えるほうが精神衛生上良い。
なぜなら研究者として、いつもいつも最上のパフォーマンスを出せる環境が得られるとは限らないであろうし、1つ目の道(どう)のみを追い求めてばかりでは息苦しくなってしまうからだ。(y=)log(x)関数のようにサチュレーションする(saturation、頭打ちになる)グラフを想像してみよ!となりあう点と点とをy軸上に射影してみれば、xの値が増加するにつれ射影された点と点との距離はどうしても密集してしまうことに気づけるはずだ。
研究において問題を解くことに成功したかどうかの定義はその問題に対して意欲を失うことなくどれだけ努力を印加(input)することができたか(、そのプロセス)である。その問題に頑張って取り組んだプロセスがそこにあるのであれば、その結果たとえ解けなくても成功、逆に努力なしで解けてしまったのならば、それは成功したとは言わない(元同僚の先生より)
何も考えずに確信のない状態で出した答えが幸運にもたまたま正解であったということがある。他方で熟考に熟考を重ねた挙句に、確信をもって導いた答えが、結果的にたまたま誤ってしまっていたということも世の中にはあり得る。この場合、仮にその答えが間違っていたからといって、その熟考のプロセスまで何ら価値がないものだと簡単に切り捨ててはいけない。
たとえ答えが誤っていたとしても確信をもって導いた答えへと至る熟考のプロセスには大きな価値があり、貴重なものであると捉える姿勢が重要である。多くの場合、熟考に熟考を重ねて確信をもって導いたプロセスは、たとえ間違っていたとしても確信をもって修正され、確信に満ちた次のプロセスへと生かされ、つながってゆくはずである。(その人あるいはそのアルゴリズムの)確信度を知ることはかくも重要である!
人生において成功したかどうかの定義もまた同様であろう。すなわち、
人生において成功したかどうかの定義は自分の人生を全うするための本質的(intrinsic)なプロセス(人生を全うするためのバックボーン)に対してどれだけフォーカスして、そこに対して意志(will)を集中して努力を印加(input)して爪痕(つめあと)を残すことができたか(、そのプロセス)である。
意志(こそ)は(連続無限の濃度を生み出し、時に不可能を可能とする奇跡の)力である!
Where there's a will(人生を全うするための固有値),there's a way(人生を全うするための固有(関数)ベクトル(空間)).
Abraham Lincoln (1809 - 1865)
自分の人生を全うするための本質的な課題に対して根気よく、意志を集中・集積しながら心のなかに折れることのない一本の槍(人生を全うするための固有(関数)ベクトル)を宿して頑張って取り組んだ濃密なプロセス(自身の人生に固有なベクトル空間)が(縮退することなく)そこにあり、爪痕(つめあと)を残すことができたのであれば、その結果たとえ解けなくても成功、逆に努力無しで解けてしまったのならば、それは成功したとは言わない。
すなわち、ぎっしりと中身(contents)や内実(fruits)の詰まった(数学でいうところの)稠密(ちゅうみつ、ちょうみつ、dense)、さらには間隙(かんげき)や穴が全くない完備(かんび、complete、甘美!?)な真に実のある自身の人生に固有なベクトル空間が縮退(しゅくたい)することなくそこにあるのならばそれで良しとするモノの観方・考え方・捉え方・発想の仕方・世界観である(1より大なる固有値とともにあるのであればなおさら良い.why 1より小なる固有値のもとでは、べき乗すると空間が縮退してしまうから、、、)!(固有値が)1より大きいのか小さいのか、それが問題だ!
(人生を全うするための固有値が)To be (greater than 1), or not to be, ― that is the question.
(in Hamlet, William Shakespeare, 1564-1616)
生きるべきか(人生を全うするための固有値が1より大きいのか)死ぬべきか(小さいのか)、それが問題だ
(ハムレットより, ウィリアム・シェイクスピア, 1564-1616)
(例)ウイルスにとっても実効再生産数(R)という固有値が1より大きいのか(小さいのか)、それが問題だ
ここで稠密(ちゅうみつ)であることと完備(かんび)であることとは概念として一線を画している(singularityがあり、位相的に異なる!)ことを明確に意識しておきたい。『ぎっしり中身が詰まっており、なおかつ間隙や穴がない』ことが完備である。
たとえば有理数全体の集合はある有理数のつぎの有理数を指定できない(指定した瞬間に、それよりもさらにより近い有理数が生じてしまう)くらいに隣どうしがぎっしりと詰まった稠密集合であり、いかなる無理数に対してもいくらでも無限にアプローチして近づいてゆく(接触する)ことさえできる(有理数列の極限が無理数を含むあらゆる実数を析出する!)のだが、その中にはやはり、無理数という無数の間隙や穴を内包してしまっているがために完備とまでは言えない。
その意味では(実数と同じ連続無限の濃度をもつ)無理数であってもまた、そのなかに有理数という間隙や穴を無数に内包してしまうのであるから完備とまではゆかず、稠密集合の範疇(はんちゅう)にとどまってしまう。他方、有理数と無理数を合わせた実数全体の集合においては間隙や穴が全く存在しえないために完備であると言いきれる。完備であることは大黄河からひと雫(しづく)、アラビア砂漠からひと粒をみつけるがごとく、解析的な解の存在を安定的に保証するうえで数学的に(あるいは安全・安心という観点では一点の死角もないことが心理学的にも!)極めて重要である。稠密であることが決定的(本質的)に重要なのか?それとも完備性まで求めるのか?問題に応じてそこを見極めることが重要であろう。
解の存在に関して言えば、『代数学の基本定理』によるアプローチも本質的に重要である。実係数の代数方程式であっても、かならずしも実数の範囲内に解がみつかるとは限らない。他方で、これを複素数の範囲まで拡げて考えれば、任意の代数方程式(複素数係数であってもよい)は複素数の範囲にかならず解をもつことが知られている。『代数学の基本定理』は19世紀にCarl Friedrich Gauss(1777-1855)によって証明された。線形代数において、直観・幾何学・野性的に見通しよく単純・明解にハンドリングすることができる直交行列の普遍・一般・抽象化、複素数拡張としてのユニタリ行列による完備化、対称行列の複素数拡張としてのエルミート行列による完備化が重要になってくるゆえんでもある。
任意の正方行列は交代(反エルミート)行列と対称(エルミート)行列との和にかならず分解できるという事実もこれまたきわめて重要である(直観的には驚くべき事実である!)。(力やモーメントといった)あるベクトル場を考えるとき、交代行列は原点を中心とする微小領域の瞬間(ねじり)回転(変形運動)力(モーメント、トルク)と対称行列は原点を中心とする微小領域の対称的な伸び(縮み)(垂直ひずみ)(変形運動)力とそれぞれが剛体の運動(群)を記述する際によく用いられるユークリッド運動群でいうところの並進運動(技)と回転運動(技)とに対応しているのだ。
瞬間(ねじり)回転(変形運動)力(モーメント、トルク)は微小領域(コントロール・ボリューム)を構成する面に対してせん断ひずみ(skew)(変形運動)をもたらすことから、交代行列はひずみ対称行列ともよばれる。医療工学においてもモーメントによる生体のひずみあるいはせん断ひずみ変形運動を考えるうえできわめて重要である。率直な数学的表現が物理の本質を垣間見せる好例といえよう!
A = \dfrac{A + A^T}{2} + \dfrac{A - A^T}{2}(例)風船に針の穴ほどの穴が空いていたとしても、トポロジー的にはそれはもはや球面とは言えず、もはや円板と同相になってしまう。小さな穴ひとつあるかないかが本質的かつ決定的な位相の分かれ目となりうる。
研究者は概して浮世離れして見えるものだが、けっして上(うわ)の空になっているわけではない。ただ自身の土俵内(時には土俵外のこともある!)の何処かに爪痕(つめあと)を残すべくフォーカスしており、そこに対して孫悟空よろしく心の中に折れることのない、まさに中国の伝奇小説『西遊記』に登場する如意金箍棒(にょいきんこぼう)の如(ごと)き一本の槍を宿して意志(will)を集中・集積して『連続無限の!』努力を印加(input)しつづけているだけである!
You have to trust that the dots will somehow connect in your future. (Steve Jobs, この点と点とが兎にも角にも将来において結びつくという信念をもたなければならないのです。)
ここで、点と点とが多すぎる場合には、結びつける場合の数(nCk)が爆発的に増加してしまうため、その選択が困難になることには留意されたい。似たようなメニューがたくさん並んでいるレストランでは選択が大変困難な作業になるのだ!
Steve Jobsは大学で学んだカリグラフィーの技術をマッキントッシュを開発するときに、フォントとして組み込んだのである!すなわち、『行きかふ年』と『年』とがSteve Jobsの頭のなかで出会うことで相互にコミュニケーション・リンクによるモーメントを与え合い、化学融合反応を起こしながら『結びついた』ことによりマッキントッシュの美しいフォント(字游工房によりデザインされたヒラギノフォントなどは秀逸である!)が生まれたのである!
囲碁の布石において、最初は悪手に見えた手が、後々振り返ってみれば実は好手であったということが時に起こりうる。ひとつのコミュニケーション・リンクを見ているだけでは悪手にしか見えない手であったとしても別のコミュニケーション・リンクを見出すことさえできれば活路(かつろ)に転じうる可能性は十二分にあるのである!重要なのは世界観だ!!!!
(例)たがいに相似な行列は、どれも同一の線形変換(事象(じしょう)、出来事)のいろいろさまざまな基底(きてい、世界観)に関する行列による表現である。
(例)座標変換と運動変換の統一・統合的かつメタ的なハンドリング
『手先の(基底)座標系(たとえば臓器座標系)に埋め込まれた位置ベクトル(たとえば臓器内の患部(腫瘍)の位置ベクトル)を座標変換して根元の(世界)座標系に埋め込まれた位置ベクトルとしての(座標)表現を得た』という世界観と、『当初、根元の(基底)(世界)座標系と一致していた、手先の(基底)座標系(たとえば臓器座標系)に埋め込まれた位置ベクトル(たとえば臓器内の患部(腫瘍)の位置ベクトル)が、手先(基底)座標系の運動(変換)にともなって、一緒に運動した結果、あらたな座標へと移動した』という2つの事象は(根元の世界座標系に対する手先座標系に埋め込まれた位置ベクトルの)相対的な位置(移動)の変換(行列)によって同様に表現されるという観点では統一・統合的にまったく同様の表現が可能で、一段抽象化の階段をのぼることで、普遍・一般・抽象的かつメタ的にハンドリングすることができる。
未(いま)だ基底(きてい)の定められていない座標系に正規直交(せいきちょっこう)なる基底を選べば、それらの基底は(実は!)単位行列を構成する列ベクトルである単位ベクトルとして座標表現されることになる。これは、自分自身(と一致する座標系)を自分自身(と一致する座標系)に写(うつ)す座標変換(恒等変換)行列が単位行列で定められることによって確認(check)することができる。
本来、世界座標系の基底ベクトルは正規(大きさが1)で直交してさえいればそれでよいのだから、さまざまに自由な表現が許されてしかるべきではないか!と一見、思ってしまいがちなところではある。ところがどっこい、これはあくまで見せかけだけの自由であり、座標変換行列、特に恒等変換行列を導入することによってこのような自由への幻想(げんそう)は無残(むざん)にも打ち砕かれ、これとの辻褄(つじつま)を合わせるべく基底表現の多様性が排除(自由度が拘束)され、結果的に単位ベクトルとして一意に基底の座標表現が定まってしまうことになる。現実の掟(おきて、拘束)はかくも厳しいのだ、、、一は全、全は一※である!
他方で逆説的ではあるが、世界座標系(基底)をどのように取るかは本質的かつ決定的に重要である!あらゆる価値観や感性は、その人の心の持ち方(世界座標系(基底)の取り方)によって、いろいろさまざまなものに変現してゆく事※に気づいた時(そうあるからこそ、逆説的ではあるが適正な基底を定めることがかくも重要になってくるのだ!)、その人は真実を見ることが出来るのだという(『華厳経(けごんきょう)』の最も大事な部分である如心偈(にょしんげ)の中の一節)。まずは基底を適正に定めてみよう!そうすれば適正な座標値が定まる(得られる)であろう!
※具体的にたとえば『磁界は電界の相対論的効果である!』と捉えるアインシュタインの世界観がある!
(例)たがいに相似な行列はどれも同一の線形変換(T)のいろいろさまざまな基底(φ_A)に関する行列(T_A)による表現と捉えることができる。すなわち、基底(座標系・視点(perspective))をいろいろさまざまに取り換えて同一の線形変換(T)を眺めて観たとしても固有方程式(モード)の係数から導かれるDeterminant(変換前後の体(面)積比)やTrace(固有値の和)といった量は不変(特徴量)である!
(例)適正な医用画像(断面)を得るうえでも適正な基底(座標系)を定めることが重要である。そうすれば適正な座標値(診断の特徴量)が定まる(得られる)であろう!
※アニメ『鋼の錬金術師』では『一は全、全は一』とは何かと師匠から問いかけられたアルとエドが無人島に放り込まれ、そこでサバイバルするなかで万物(ばんぶつ)の流転(るてん)を体感(たいかん)し、世界の真理の断片(だんぺん)を見出した。
(師匠からの問い)一は全、全は一(One is ALL, ALL is One)とは?
(アルとエドの回答)全は世界、一はオレ(ALL is the WORLD, One is Me)
ここで、要素が関係性(コミュニケーション・リンク、超偉大なるテンション(超万有引力!))や(これにもとづく社会)構造をつくる、あるいは関係性や(社会)構造が要素に役割を与えるという具合に、因果関係は互いに逆方向に働いていることに着目されたい。
将棋の格言に『金底の歩、岩よりも堅し(きんぞこのふいわよりもかたし)※』というものがある。囲碁と同様、将棋においてもまた、コマとコマとの間のコミュニケーション・リンク(およびそこで働く超偉大なるテンション(超万有引力!))をつくり、取られたら取り返すことができる状態にしておくことが戦略上、あるいは安全保障上、きわめて重要な作業になる。サルの世界でさえ、仲間のサルが殴られれば、仲間が殴り返しにゆくのだという。特に将棋の解説では『(あるコマにある)コマを紐(ひも)づける』という言い方が用いられることが多い。
※運動学的にはなに(がし)かを掴(つか)めば(あるいは手放せば)機械的インピーダンス(慣性・粘性・剛性)が増大(減少)し、固定・安定化(機動(きどう)・非安定化)できる。『溺(おぼ)れる者は藁(わら)をもつかむ』、『転んでもタダでは起きるな(武器になりそうな石っころでも拾っておけ)』の精神!であり、そのようなイメージ、感覚を持っていることがわれわれにとって人生戦略上も有効であろう、、、
月日は百代(はくたい)の過客(くわかく)にして、行きかふ年もまた旅人なり。舟(ふね)の上に生涯(しょうがい)をうかべ、馬の口とらへて老(お)いをむかふるものは、日々旅(プロセス)にして、旅を栖(すみか)とす(松尾芭蕉、奥の細道)
失敗(エラー)経験を積まず、ただ成功体験のみにもとづいて導出された手法(あるいはシステム)は中長期的にみれば、頑健(がんけん:robust)性がなく、むしろ脆(もろ)い(fragile)とさえ言えよう。濃密(dense)なプロセスとしての失敗(エラー)経験の集積(accumulation)は未来への投資によって得られた偉大な資産(asset)である。
教訓化されたプロセスとしての失敗(エラー)経験と成功経験とを両方(構造として)織り込むからこそ、頑健かつ高性能なシステム(の構造)を構築してゆくことができるのだ。すなわちシステムに対して良質のフィードバックを与えうるものは成功体験プロセスの集積ではなくむしろ、濃密な失敗(エラー)経験プロセスの集積なのだ!
換言すれば、失敗(エラー)の集積からその構造を学び、これを織り込むことこそが、頑健かつ高性能なシステムを産み出すうえでは本質的に(intrinsically)重要なのだ。
(例)失敗(エラー)経験を何度も繰り返しながらジワジワとタスク軌道を連続的に変化・変容させつつ
失敗(エラー)と成功の間に相を入れる特異点(あるいはその集合としての線)の存在を探る。これを繰り返せばタスク軌道を洗練・進化させることができる。
素人は特異点を扱いが困難で得体の知れないものとして、忌避(きひ)しがちな傾向にあるが、(数学の)プロは扱いが困難で得体の知れない特異点の付近でこそ、なにがしか重要な手がかりが隠れていやしないかと刮目(かつもく)してよくよく調べようとするという。
これはわれわれがさまざまな場面で無意識あるいは意識的に行っていることだが、このメカニズムについてより深奥に迫るためには特異点をまたがずにジワジワと軌道を変化できるものを同相として取り扱うホモトピックの概念を知っておくとなお良いであろう。この方法はロボティクスにおける学習方法としても研究されている(深層強化学習、ポテンシャル法など)。(ジワジワ変化による特異点探索法)
これはRudolf Emil Kalman(1930-2016)が提唱し、ばらつきのある過去のデータの集積を参照、フィルタのパラメータを逐次更新するカルマンフィルタの原理に類似(similar, analogous)である。カルマンフィルタは目標物の時間変化を支配する物理法則(たとえば等速直線運動)を活用して、本来連続的かつなめらかな運動軌道を有しているにもかかわらず、(多くは正規性の)ばらつきをもつノイズに汚染された状態で観測される目標物の位置を過去(内挿あるいは平滑化)、現在(フィルター)、未来(予測)にわたって効率よく推定することができる。
Herbert William Heinrich(1886-1962)によれば、およそ300回に1回は(ヒトにとって)想定外な事(象)が起こる。子供が波にさらわれてしまうのはこの、およそ300回に1回おこる(ヒトにとって)想定外の大波が来たときであるという。これらに対して頑健(robust)なシステムを構築するためには失敗(エラー)経験プロセスの集積が欠かせない。
そうしてまた、成功経験プロセスのみならず、失敗(エラー)経験プロセスをも教訓化して構造(mechanism)として織り込んだシステムには一種独特の雰囲気(aura)や迫力(force)、何とも言えない魅力(charm)や温かみ(warm)があるものなのである。
なぜならそのようなシステムを構成するパーツのひとつひとつにこそ、熟成された人生の妙味(みょうみ,fascination)・薬味(spice)や究極の人間らしさ(humanity)がぎっしり詰まっていることを感じとることができるからだ。
失敗(エラー)することには耐えられるが、挑戦しないでいることには耐えられない。成功を学ぶためにはまず、失敗(エラー)(の構造)を(プロセスとして)学ばなければならない。人生でなんども失敗(エラー)してきた(。もちろん、現在も新しい挑戦をしつづけているのだから当然、失敗しつづけている、その継続的なプロセスの集積がある)からこそ私は成功した(/つづけている)。(マイケル・ジョーダン)
『挑戦しないでいることには耐えられない』、『失敗(エラー)(の構造)をプロセスとして学ぶ(機序・構造論研究にこそ価値がある!)』というモノの観方・考え方・捉え方・発想の仕方・世界観がすばらしい(これこそが鍛錬・洗練の賜物であろう)!すなわち、いろいろと思いついたら何でもトライしてみて、たとえ失敗(エラー)したとしてもそこから機序・構造論研究においては世界観学習に資する良質のフィードバック(失敗のメカニズムを抽出し、これを分解・再構築すること)が得られて、結果として少なくとも鍛錬・洗練されたプロの世界観が残る(それで十分ではないか!?)のだから、結果を恐れて挑戦しないでいる理由はこの世のどこにもないのだ!換言すれば、挑戦しないでいることこそが最大の失敗(エラー)なのだ!!!!そうして失敗しつづけながらも、同時に挑戦し続けることができている人は(観る人が観ればとっても!とっても!とっても!とっても!)魅力的なのである。
人生に失敗(エラー)がない(挑戦しないでいる)と人生を失敗(エラー)する(斎藤茂太)
Success is the ability to go from one failure to another with no loss of enthusiasm.(Sir Winston Leonard Spencer-Churchill)
成功とは(野性・野能に突き動かされながら挑戦する、人生を全うするための固有値たる)意欲を決して失なうことなく(みずからの人生を全うするための固有(関数)ベクトル空間において)失敗(エラー)につぐ失敗(エラー)を繰り返すことで失敗(エラー)(の構造)をプロセスとして学ぶ(機序・構造論研究にこそ価値がある!)ことである(そうすれば必ず鍛錬/洗練された良質のプロの世界観が残る!それで十分ではないか!?)。(サー・ウィンストン・レナード・スペンサー=チャーチル)
すなわち、
0.やらずにはおられないこと(固有(関数)ベクトル)を見つけてしまったがために
1.(固有値が膨らみ)挑戦しないでいることには耐えられなくなり
2.さらには、へこたれることをあきらめ
3.ついには、あきらめることをあきらめる羽目になる!
Even a mistake may turn out to be the one thing necessary to a worthwhile achievement. (Henry Ford,失敗(エラー)とは、よりよい方法で再挑戦する素晴らしい機会である。)
I didn't see it then, but it turned out that getting fired from Apple was the best thing that could have ever happened to me. (Steve Jobs,そのときには分かりませんでしたが、Apple社からクビにされたことは私の人生で起こり得た最善の事になったのです。)
A broken bone is the stronger when it is well set.(うまくつながれば折れた骨は以前よりもずっと丈夫になる)。
弘法も筆を誤り、猿も木から落ちるのである!失敗(エラー)経験や挫折経験を恥ずかしいものと捉える風潮(世界観)からは距離をおいて(
Off to see the world !)、いち早くこれを脱却するのが吉(よし)である!
失敗(エラー)が起こってしまったことは決して悲しむべきことではない!むしろこれを契機として、『チャレンジは誇るべき偉大な未来への投資であり、濃密なプロセスとしての失敗経験の集積はチャレンジしたからこそ獲得できた、手法(あるいはシステム)の頑健性を向上するための誇るべき偉大な資産』と捉えうる思考(世界観)の(大)転換を図るべきであろう。一切は心に従って転ずる!
失敗(エラー)経験プロセスは成功の母であり、みずからの骨身(ほねみ/こっしん)にしみた(ほろ苦い!)失敗(エラー)経験プロセスにもとづく教訓はきわめて大きな説得力をもつ。換言すれば、説得力のある偉大な教訓は成功経験からではなく痛みを伴うプロセスとしての実際の『生きた失敗(エラー)経験(談)の集積』からこそ生まれるのだ!(しくじり先生法)
失敗(エラー)を恐れるな!恥ずかしがるな!失敗(エラー)経験は積極的に共有化せよ!
人間がたったひとりでできることなんて高々知れている。ひとりひとり、長所もあれば短所もあろう。みずからの短所を補完(間)・外挿してくれるのは、周囲の人・物である。これを踏まえて失敗(エラー)経験を人間(じんかん)において複数の多様な人間(軸)で『群知能(ぐんちのう)として共有化』するやり方は有効な方法であろう(これはインターネットのもつ破壊的インパクトを観れば納得がゆくであろう)。
これにより、助言・助力が相互に得られて解決に向かう問題もあるのだ!なぜなら、蛇(じゃ)の道は蛇、餅(もち)は餅屋であり、その道の真のプロフェッショナルとはだれよりもその道についての多くの構造化されたプロセスとしての、言わば『珠玉の失敗(エラー)経験(談)集』を教訓化して語れる人でもあるからだ。そうしてまた、その多くは自らの骨身にしみたほろ苦い失敗(エラー)経験プロセスの数々なのだ、、、
(ひっくり返して考える:長所と短所はオモテとウラの関係)~~~~~~~
就職担当の面接官からよく聞かれる質問として、『あなたの長所と短所はどこですか?』というものがある。長所はまあよいとして、短所の返答に困った経験はないだろうか?長所や短所は同じ性質(特性・属性)に対する捉え方(世界観)の問題である。原子力にも平和利用と兵器利用の両面があるように長所と短所はオモテとウラの関係にあり、長所は短所として捉えることができるしまた、短所は長所として捉えることができるのだ!
面接官が問うているのは、まさにこのオモテウラの関係をよく理解し、長所と短所をひっくり返して考えうる発想の柔軟性を有しているかどうか?ということである(余談だが、ワイシャツを脱ぐ際によく腕の部分が自然とまくれて表裏ひっくり返ってしまうことがあるが、洗濯機にはそのまま表裏ひっくり返した状態で突っ込むのが簡便である。なぜならアイロンは衣類の裏側からのほうがかけやすいからである。スラックスも同様である)。さらにまた、この発想の柔軟性を局面(Time Place Object Human-Things:TPOHT)に応じて使い分けることができれば満点である。
ところでアイロン台にワイシャツを置くと、あちらこちらに凸凹(でこぼこ)ができていることに気づく。この凸凹を解消するためにわれわれは、ワイシャツの端と端を持って、引っ張りながらアイロンをかける。この柔軟な発想に基づく偉大なアイロンがけの手法はトポロジーという学問においてもその起点・原点・出発点(starting point)・一丁目一番地・根本であり、なおかつ根幹でもあるというべき本質的にきわめて重要な手法である!
彼(か)の有名なポアンカレ予想を解くために、 グレゴリオ・リッチ=クルバストロ(Gregorio Ricci-Curbastro)は3次元多様体の凸凹を上記のアイロンがけ手法により均(なら)すリッチ流(Ricci flow)の概念を思いついた。
ハミルトンはこのアイロンがけの手法を2次元多様体に応用展開し、『その上にあるあらゆる閉じた曲線を点に縮められるような凸凹な面』を均(なら)してゆくと最終的には至るところ均(ひと)しい曲率をもつシワのない曲面である球面になることを突き止めた。
しかしながら、3次元多様体をアイロンがけした場合には、多様体の切れ端が集まっているような場所においてところどころ、どうしてもシワがよってしまうことがある。これを回避する方法を見出したのが彼(か)の有名なペレルマンである!ペレルマンは多様体の切れ端が集まり、どうしてもシワがよって(もつれて)しまう部分を切り取って、アイロンをかけて(もつれをほどいてから)から、再びもとに戻して縫い合わせるという画期的な外科的手法を思いついたのである。
一方でサーストンはこのときすでに、
『宇宙がたとえどんな形であろうとも、それは必ず、最大で8種類の異なる断片から成り立っているはずだ』
という予想を立てていた(サーストンの幾何化予想)。この『サーストンの幾何化予想』によって、宇宙がとりうる形は、最大でも8種類であるということを証明することへと焦点は移った。すなわち、『サーストンの幾何化予想』を解けば、おのずと『ポアンカレ予想』も解かれることになるというのだ。
上記の経緯を踏まえてペレルマンは『サーストンの幾何化予想』、アイロンがけの手法、並びにもつれをほどくための画期的な外科的手法を巧妙に繋(つな)げ合わせ(、まさに超偉大なるコミュニケーション・リンク(時空人間を超越した超偉大なる超張力、言わば『超万有引力!』)を貼)ることで、宇宙がとりうる形は、最大でも8種類であるという『サーストンの幾何化予想』の証明にまで漕(こ)ぎつけることができ、その帰結(きけつ)としてポアンカレ予想が解決できることを首尾(しゅび)よく証明して見せたのである!
Outside in
上記を踏まえて、この問に対しては、自身の長所とおもわれる性質(特性)について、これを短所として捉え直した場合にどのような副作用がありうるか?を客観的に検討、よく理解していますよと答えれば気がきいていて良いのではないだろうか?
たとえば、『ものごとを突き進めて、とことん最後までやりぬく、という私の長所には、視点・視座を変えてみれば、何事も必要以上にやりすぎてしまうという副作用が随伴(ずいはん, adjoint)していることを(私自身も客観的に)よく認識していますよ』と答えるのだ。
そうすれば面接官は、『こいつは物事を多面的に捉えられる、頭のやわらかい人間だ(イノベーションは複数の世界観がぶつかり合い、化学反応したときに起こりやすい!)』と高く評価してくれるだろうしまた、短所の裏返しとしてみずからの長所をさりげなくアピールすることにもつながる。もちろん
相手の面接官が柔軟な思考の持ち主であれば(超重要!!!!)の話だが、、、
~~~~~~~(ひっくり返して考える:長所と短所はオモテとウラの関係)
(思考展開するうえでの前提条件について)現在の持ち札が不足しているだけで、未来には充足しているものと想定する(なぜなら、未来に充足していたら、その世界はきっとおもしろい世界になっているだろうから)。
(例)現代の65歳以上の老人にはスマートフォンの操作が苦手という前提があるが、果たして20年後の老人においてはどうなっているであろうか?
想像力をフルに働かせて、未来に充足しているであろう技術水準をも見据えたうえで中長期の将来ビジョン(未来の本質・骨格)を描く。そこ(
未来の本質)
に向かってわれわれのコア基盤技術を投入、つなげてゆく。
(例)王貞治監督はバッティングの理論として、みずからのバットの軌道とボールの軌道とを頭の中で想像して、その交点に対していかにタイミングよくバットのスイートスポットを(モーメントの勢いよろしく)ぶつけてゆけるかということについていろいろと思考を巡らせながら素振りの練習を繰り返したそうである。
(例)申請書を書くときも審査員がその申請書に対して推薦文を作成する作業をサポートする助手のような立場で観て、適切な情報を申請書の適所に織り込んでゆくことを心がけながら推敲を重ねるべきであろう。
(サブ手段1)根拠(Why?)のある、自分なりのやり方(How?、方法論、構成論、構築論)を日々改善しながらモノゴトに対してとことん突き進み、やりきり、つなげきる(とことん突き進み、やりきり、つなげきる法)。
(サブ手段2)行動せずにあきらめるのではなく、行動しながら(視点や切り口を変えながら)考える。まずは行動し、視点や切り口を変えてモノゴトを観ることで情報量が増加、これを踏まえてモノゴトを最も統一(一貫)・統合(包括)・普遍(一般)的で(unitary & comprehensively & universally)、直観(幾何学・野性)的に見通しよく(intuitively & topologically & wildly imaginable)単純・明解で(simple & crystal clear to understand)、だれもが簡便・快適で(easy & convenient & comfort)随意(自由自在、at will)に、なおかつ安全(safe)・安心(secure)・安定的に
( Me-DigIT 魂のこもった!)思いやり(stable & considerate)をもってハンドリングできる視点や切り口(viewpoints and sections)を探る。
エミー・ネーターが研究を通じて道しるべとした行動原理は、つぎのようにまとめられるだろう。
『数や関数や演算どうしの関係性(つながり、コミュニケーション・リンク、そこで働く超偉大なるテンション(超万有引力!))を明瞭化して、統一(一貫)・統合(包括)的に適用できるようにし、その生産性を最大限に引き出すには、それを特定の対象から切り離して、普遍・一般・抽象的に有効な(メタ的な)概念として(再)表現しなおさなければならない。』
そうしてこのオブジェクト指向的な行動原理は、デジタル化ときわめて相性が良いのである!
(参考文献)
イアンスチュアート,数学の真理をつかんだ25人の天才たち,ダイヤモンド社.
(例)標準形で与えられた二次曲面がどのような曲面であるかはまず、座標軸に直交する平面の切り口で考えることを発想の起点・原点・出発点とすればわかりやすい。
(例)ゼロを自然数として認めるべきかどうか?という立場(positioning, stance)の問題がある。ゼロを自然数として認めてしまうと、1番目の自然数がゼロ、2番目の自然数が1ということになってしまい、ハンドリングの際に混乱を生じやすい。自然数を統一・統合・普遍・包括的で直観・幾何学・野性的に見通しよく単純・明解で簡便かつ随意に安全・安心・安定的に( Me-DigIT 魂のこもった!)思いやりをもってハンドリングするためには、認めない立場のほうが実用上、一般に普及しそうだが、、、
(例) Γ(n+1)=n!
階乗の一般化であるガンマ関数も定義の問題で1ずれていることには注意が必要である。ガウスはこのズレを修正したπ関数の定義を提案している。こちらのガウスのπ関数のほうが、直観・幾何学・野性的に見通しよくハンドリングしやすい。
さて、我々の研究室の軸は『 医療のデジタル化(医デジ化)』である。
『医療・バイオは新しいデジタルだ!』を発想の起点・原点・出発点(starting point)・一丁目一番地として旗印に掲げ、
人工知能・IoT・ロボット技術を 医療・ヘルスケア・バイオ分野に展開して、
超高度に『医デジ化』された社会 (Highly Ultra Me-DigIT Society) をゴールとして実現すること
がわれわれの研究室の使命(our mission)である。
医療支援システムに限らず、一般のシステムにおいて、
① 統一(一貫)・統合(包括)・普遍(一般)的で、
Unitary & comprehensively & universally
② 直観(感)(幾何学、野性)的に見通しよく、単純・明解で
(Don't think !!!! Feeeel !!!!)
Intuitively & topologically & wildly imaginable,
simple & crystal clear to understand
③ だれもが簡便・快適で随意(自由自在)に安全・安心・安定的に( Me-DigIT 魂のこもった!)思いやりをもって
Easy & convenient & comfort & at will & secure & safe & stable & considerate for everyone
扱える(ハンドリングできる)
ことがシステムを開発・実装・製品化して、これを広く一般に普及するうえで、本質的(essential)かつ決定的(crucial)に重要である。上記を踏まえて我々は、医療のデジタル化(医デジ化)を提唱している。なぜなら、デジタル化は上記の要件ときわめて相性が良いからだ。
19世紀にGeorge Booleが切り開いたデジタルの道は今やなんと、医療・バイオの荒(広)野にまで及びつつあるのだ!!!!
さらに言えば、上記の要件を医デジ化により極限まで満たすことがわれわれの最終目的地たる『超高度に医デジ化された社会』およびそこで具現化される『超高度に医デジ化された医療支援システム』の究極型である。
さて、今後われわれの目指すべき世界(観)として
『旧時代的解析医学からの脱却』と『新時代的(デジタル)解析医学の推進』とが挙げられる。
統一・統合・普遍的で直観(幾何学、野性)的に見通しの良い近代(デジタル)解析医学の道を切り開き、これを推進するべきである。
これにより、医療・バイオを長い修練の後に初めて身につく個別具体的な職人技から医療デジタル機能関数化により誰もが簡便・快適で安全・安心・安定的に( Me-DigIT 魂のこもった!)思いやりをもって、随意(自由自在、at will)にハンドリングできる単純・明解なものとすること、またその帰結・成果として、10-20年後の日本(および世界)の医療技術水準をさらに飛躍・底上げさせ、なおかつ持続可能なものにしてゆこうとするのがわれわれの目的である。
具体的に17世紀においてデカルト、フェルマーが幾何学に座標系を導入した発明によって18世紀に線形代数学、微分積分学、(数学界における至宝、世界遺産たる絶景の宝庫である!)複素解析学などの解析幾何学(ニュートンが命名)に関する分野が急速に発展した。微積分を実数から複素数へと拡張したのはコーシー、複素解析にトポロジー的手法を導入したのはリーマンである。
これと同様に医療に座標系を導入して
デジタルを常用化(regular use of digital)することで新時代的(デジタル)解析医学を急速に発展させることができるものと期待している。その起点・原点・出発点となる一丁目一番地は臓器の輪郭形状をパラメトリックに抽出して、その形状・大きさをまずはデジタルに解析できるようにすることであろう。
そこからさらに、人工知能・IoT・ロボット技術の応用展開によりデジタル・モデル化された医療専門家の知性・知能を同じく医療専門家の肌感覚(感性・感能)にうまく従わせることができるのではないかと企図(きと)・期待している。
すなわち、医療専門家の肌感覚に近い医療専門家の知性・知能をデジタル・モデルとして再構築して、その社会実装を図ろうというのが、われわれの
『医デジ化(Me-DigIT)プロジェクト』に他ならない。
ウォルト医デジ化ワールドともいうべき医療・ヘルスケア・
バイオの楽園を我々とともにいざ築かん!と思われる方はぜひ我々までご一報たまわりたい!!!!
ここで、以下の対になる語句の意味するところは大きく異なり、一線を画していることを明確に意識しておきたい。
『
原理的にできること』と『簡便/随意(自由自在、at will)で安全・安心・安定的に
( Me-DigIT 魂のこもった!)思いやりをもって
実行できること』
『装備(一式)があること』と、『装備(一式)が簡便/随意(自由自在、at will)で安全・安心・安定的に( Me-DigIT 魂のこもった!)思いやりをもって扱えること』
『表現できる(伝える)こと』と、『簡便/随意(自由自在、at will)で安全・安心・安定的に( Me-DigIT 魂のこもった!)思いやりをもって表現が受け入れられる(伝わる)こと』
行動することの副次的な効果として、行動がトリガーとなってドーパミンやアドレナリン(野性・野能)が分泌され、頭を回転させると、さらにどんどん分泌されることが挙げられる。ドーパミンやアドレナリン(野性・野能)の助けも借りて、頭の回転がフル回転に達したところで、何かが起こる!と固く信じる!
人間の教養とは野性・野能を失うことではなく、(知性・知能とのコミュニケーション・リンク生成によって生命の神髄(クイントエッセンス)たる)野性・野能を(変容・)洗練(・進化)させることである(知性・知能とのコミュニケーション・リンク生成による野性・野能の変容・洗練・進化法)。
岡部伊都子
ここで、仮にたとえそのときに何かが起きたように感じられなくとも、がっかりしないことにする!(がっかりすることをあきらめる!)。決して無駄な行動や思考をおこなったわけではなく、将来的に(超万有引力!がにわかに働きだし)なにかが起こることにつながっている(偉大なるコミュニケーション・リンクが張られた!)に違いない!
今この瞬間に(超万有引力!が時空人間を超えてにわかに働きだす、)そのためのコミュニケーション・リンクたる伏線(ふくせん:foreshadowing)を未来に向けて張り、布石(ふせき)を打った(laid the foundations for future development)のだ!と固く信じることにする!『江戸の仇を長崎で討つ』ということわざよろしく、伏線(ふくせん)や布石(ふせき)は長い人生(あるいは死後までも含めて)、将来においてこれを回収したり、効力を発揮させればそれでよい(という風に考える)のである!
点(dot)と点(dot)とが『つながっている』と考えるか、あるいは『つながっていない』と考えるかは(実は、なんと!)世界観(見解)の違い(だったの)であり、両方の世界観(見解)において筋道はそれぞれ一応通っていると言える。しかしながら双方の世界観によって時空人間を超えて描かれるべき世界線(導かれる結論)が大いに異なったものとなりうる可能性については注意が必要である。
(例)つながっていないと(直観的には)感じたとしても、(いや実は)つながっている(に違いない)!と捉えうる世界観が重要である!コミュニケーション・リンク(およびそこで働く時空人間を超越した超偉大なるテンション(超万有引力!))の張られていないWEBページどうしは、(皮相的にみれば)つながっていないと考えるのが一般的で自然な捉え方なのかもしれない。しかしながらこれをランダム・アクセス・リンクを含めてあらためて捉えなおせば、(実は)つながっていると捉えうる(あるいは相手に想像させる)世界観も可能になってくる。そうしてこうした世界観をうまく活用してゆくことで、より統一・統合・普遍的な(強運・強者のメタ的な)思考や群知能(ぐんちのう)構成が可能になってくると言うのである。
(例)線分の両端を無限の彼方まで伸ばした直線(あるいは開曲線)どうしは、(無限遠点という1点を加えて観ることで!)その両端が無限の彼方(かなた)でつながっている(すなわち曲率半径∞の円弧)と捉える世界観においては、正円(あるいは閉曲線)と一対一の対応がついてしまう。すなわちこのような世界観のもとでは正円(あるいは閉曲線)と直線(あるいは開曲線)との間に(なんと!)相(そう)は入らない。
これについてより詳細を知るためには、角度を保存しながら直線/正円を直線/正円に写す共形(あるいはその二つ名を等角ともいう)写像の理論やn次元双曲幾何学のモデルであり、その幾何学のもとでの各点が n次元円板あるいは球体に属し、かつその幾何学のもとでの直線がその円板に含まれる円板の境界と直交する円弧または直径によって与えられる有名なポアンカレの円板について学ぶ必要がある。
(参考文献) 富岡礼子,曲がった空間の幾何学,講談社.
(参考文献)
都築卓司,トポロジー入門,講談社,pp.155-157.
(時間軸的にも、空間軸的にも、さらには人-物間軸的にも)増えた情報をも含めて黄金のN角形ループを構築する戦略を練る(ルービック・キューブ法:ルービック・キューブを解くときにひとつの面だけを見るのではなく、キューブをクルクルまわして情報量を増やしながら解き方を考える、あのやり方である)。これはY=PXの勾配Pをクルクルまわしながらある評価関数を最大(あるいは最小)化する最適な勾配Pを探索するのとanalogousである。このときP=YX^{-1}はリッカチ方程式の解として求まる。
リッカチ方程式はロボットビジョンの理論とも関連している。すなわち、原点にロボットビジョンの視点を置けばすなわち、ロボットは原点を通る同じ傾きの視線をすべて同一の点に縮退させて捉えているということになる。Goshはこの事実をもとに透視システム理論(perspective system theory)を展開し、運動するターゲットに対する同定および観測可能性について直観・幾何学・野性的に見通しよく単純・明解に論じている。
真正面からまっすぐ近づいてくる相手との距離感はきわめて測(はか)りづらい。どんなに相手が強くても真正面からぶつかる戦法がきわめて有効に機能するゆえんである。超音波画像においてもこれは同様であり、(3次元空間のうち、縮退していない)面内の運動は同定しやすいが、面外の(奥行方向の)運動は(超音波画像上で縮退しているがために)きわめて同定しづらい。
(参考文献)
狩野弘之,西村敏充,Riccati方程式と制御問題,J.SICE, Vol.35, No.2, 1995.
2次元ユークリッド空間の運動群E(2)による変換操作のみではどうやってもひっくり返せなかったあのiPadも3次元ユークリッド空間の運動群E(3)による変換操作を加えてあらためて考えてみることでいとも簡単にひっくり返すことができるようになるのだ!自己交差(すり抜け)を許せば2次元球面(バスケットボールやミカンの皮など、われわれがイメージする通常の球面は2次元球面である!)においては位相幾何学的(穴をあけたり、切ったり、シャープに折り曲げたりせず(特異点をつくらず))に球面の表と裏をひっくり返すことさえ可能である!
(例)楕円体面や多面体面(ポリゴン面)など、球面と同相な閉曲面は、3次元空間を面の内部と外部に分割する。カゴの中の鳥よろしく、内部の点は、たとえそれが動くことができたとして、いくらくやしがったところで面を貫くことなく外部に出ることはできない。紙面に描いた閉曲線と話は同様である。
(例)腫瘍(がん)も臓器の内膜につつまれていれば、それを貫くことなく外部にでてゆくことはできない。
(参考文献)
都筑卓司、トポロジー入門、講談社.
Outside in
また実関数の積分は複素関数の積分の一部として複素平面における実軸上の積分として高次元から捉え直すことで留数(りゅうすう)定理とよばれる強力な積分値計算手法を適用することができるようになり、しばしば計算が容易化・簡便化されることが知られている。
特に,電磁気学におけるアンペールの法則(やその普遍・一般・抽象化としてのビオサバールの法則)が複素解析における留数定理に対応していることに着目されたい。この場合、電流(単位時間あたりの電荷の通過量)が(積分路に囲まれた(積分領域内の)特異点がもたらす!Harvest(天の恵みがもたらす収穫(成果)量)たる!)留数に対応している。もちろんアンペールの法則は複素積分形式のみならず実積分形式としてもその表現が可能である。また、これにともなうグリーンの定理(やストークスの定理)とコーシーの積分定理(やコーシーの積分公式)との対応関係もきわめて重要である。
ここで、投げ縄の輪を締め上げるように積分路Cをz=aのまわりに極限までぐるぐる巻きに締め上げて縮小すると、f(z)はもうほとんど定数f(a)として扱えることをコーシーの積分公式は率直に表現している。コーシーの積分公式の見た目は一見いかつくて、気軽に扱えないような、如何(いか)にも近寄りがたい空気を醸(かも)し出してくるが(だまされてはいけない!)、その全体的構図(構造、状況、ゲシュタルト)とその意味するところを一旦わかってしまえば、世界は違って見えてくる!驚くほどシンプルかつ簡便・有用な公式である。
このようにコーシーの積分公式は特異点まわりに積分路を締め上げるとそこでの関数値を(あたかもHarvest(天の恵みがもたらす収穫(成果)量)たる!)や何かしらの結晶のごとく!)析出せしめるが、この考え方はきわめて示唆(しさ)に富んでおり、人工知能援用医療ロボット工学、医用画像工学においてもきわめて応用の効く、有用なものの観方、考え方、捉え方、発想の仕方、世界観をもたらす!
すなわち変形をともなって運動する臓器内に埋め込まれた患部(腫瘍や結石)を包含(ほうがん)するように関心領域(積分路C)をうまく抽出(われわれはこれを、ディラックのデルタ関数、コーシーの積分公式につづく、第3の抽出関数として『Me-DigIT Harvest 抽出関数』と呼ぼう!)・追従しながらバウンディング・ボックスなどを用いて捉え、これをぐるぐる巻きに締め上げてゆければ、あたかも静的(static)な世界でピン止め・ピンフォール(抑え込み)固定したかのように患部を扱うことができ、診断や治療におけるモニタリングを容易化することに大いに役立てることができる!この場合、運動する臓器内に埋め込まれた患部(腫瘍や結石)の大きさ(や広がり)が留数(われわれはこれをMe-DigIT Harvest!と呼ぼう)に対応している。
(複素積分において)特異点を左手に見て(関心領域内に特異点を包含して)積分する(ぐるぐる巻きに巻き上げる)か、右手に見て(関心領域内に特異点を包含しないで)積分する(逆方向に巻き戻す:負の方向に巻き上げるという見方もある!)かとは似て非なることであり、得られる(Me-DigIT!)果実(Harvest、計算結果)は大きく変わってきてしまうのである(複素関数の多価(たか)性の原因、リーマン面を想起せよ!)!患部を臓器内に包含しながら巻き上げるのか、包含しないように逆方向に巻き戻すのか?包含する場合、(孤立特異点的であってMe-DigIT Harvestとして)摘出して完全に除去することは可能なのか?それが問題である!
(参考文献)
Joonho Seo, Norihiro Koizumi, Takakazu Funamoto, Naohiko Sugita, Kiyoshi Yoshinaka, Akira Nomiya, Akira Ishikawa, Yukio Homma, Yoichiro Matsumoto, and Mamoru Mitsuishi, " Visual Servoing for a US-guided therapeutic HIFU system by coagulated lesion tracking: a phantom study," International Journal of Medical Robotics and Computer Assisted Surgery (IJMRCAS), Vol.7, pp.237-247, https://doi.org/10.1002/rcs.394, 2011.
A. Mariani, L. Morchi, A. Diodato, S. Tognarelli and A. Menciassi, "High-Intensity Focused Ultrasound Surgery Based on KUKA Robot: A Computer-Assisted Platform for Noninvasive Surgical Treatments on Static and Moving Organs," IEEE Robotics & Automation Magazine, vol. 30, no. 3, pp. 79-93, Sept. 2023, https://doi.org/10.1109/MRA.2022.3188221.
この効果は『低次元の束縛からの開放による効果』と呼ばれるもので、低次元の束縛から開放される次元を高次元の定義とする物の観方・考え方・捉え方・発想の仕方・世界観も存在する。
上記の考え方の応用として平面上の図形は複素平面の世界観で捉えることもできるし、単純なxy平面の世界観で捉えることもできる。もちろん両者をうまく切り替え、組み合わせながら捉えることで相乗効果を生み出すことも可能であろう。たとえば複素平面上の閉曲線は単純なxy平面で捉えること(単に世界観を切り替えて観たり、複眼視(ふくがんし)したりすること)でグリーンの定理(線積分と二重積分の架け橋となるベクトル解析の公式)が適用できることに気づく。重要なのは世界観だ!
∮C(P(x,y)dx+Q(x,y)dy)=∬D(∂x∂Q−∂y∂P)dxdy
常に問題の本質を考え、その本質を見通してから一段高い立場で解決するというのがかの有名な大数学者であるDavid Hilbert(1862-1943)の本領発揮であったという。
『低次元の束縛からの開放による効果』の具体例として、1つには彼(か)の有名なポアンカレ予想の証明は4次元以下と5次元以上とでは
アプローチ法が大きく異なる(複数の世界観をつなげたパッチワークにより解決されている!)ことが知られている。
われわれの直観に反して、4次元以下よりも5次元以上で物事を捉えたほうが証明は統一(合)的で、直観的に見通しよく単純・明解で、簡便かつ随意(自由自在、at will)にハンドリングすることができるのだ!
4次元については1982年にMichael Hartley Freedmanによって解かれ、これより難しい3次元については、2002年にGrisha Perelmanによって解かれた。
また、1つの具体例としては群知能(ぐんちのう)戦略が挙げられる。問題や課題は可能な範囲でできうるかぎりグループ全員で共有したほうがよい。なぜなら、ひとりひとりがカバーできうる解空間は限られているからだ。群知能戦略により人間(じんかん、ここでいう、人間とは世間やコミュニティのニュアンスに近い)軸の次元が高まり、結果として(実装)解空間をカバー(被覆:ひふく)できる可能性(確率)が高まる。
One human only has the power to do so much
ひとりの力(固有値)などたかが知れている
『(敬意とともに)ありがとう』と言い合える(相互感謝・相互リスペクトの)関係性の構築こそが最も尊く、『(敬意とともに)有り難い』 (そういう(相互感謝・相互リスペクトの)関係性を人間力によってうまく構築できることこそが人生戦略上きわめて重要である。)
すなわち、自分一人では決して解けないような問題も群知能(人間力の本質!)により高次元人間(じんかん)空間において直観的に見通しよく解決できる可能性が生じうるからである(3人あつまれば文殊の知恵法)。この効果によるインパクトの絶大さは、インターネットがもつ破壊的インパクトをみれば納得がゆくであろう。
フランク・ラムゼイの定理 は、コミュニケーション・リンク(およびそこで働く超偉大なるテンション(超万有引力!))によってつなげることの重要性を単純・明解に示唆している。時間、空間、人-物間をただひたすらつなげて邂逅(かいこう、出会いのこと)を増やしてゆくことに注力(ちゅうりょく)してゆければ(実は)その中にはなんと(!)、混沌のなかにもある種の好循環(positive loop)あるいは悪循環(negative loop)という秩序(order)が必然的に現われてくるということが数学的にも保証されるというのである!!!!
(例)複素関数論におけるコーシーの積分公式は正則な関数f(z)の値がzのまわりの関数値を積分することで求められることを率直に表現している。すなわち、『その人を知りたければ、まずはその人の周囲・周辺にいる友人を見てみるべき』である。
このものの観方・発想の仕方・世界観は、医療工学において臓器の運動を同定(どうてい:一意に定めること)する際にも応用展開できる。すなわち、変形をともなって運動する臓器内の患部の位置は、まずはそれが埋め込まれた臓器や周辺組織の輪郭の変形や運動状態を見てみれば、ある程度推察することができる。
(例)j不変量とモンスター群の既約表現の次元との間に不思議な関係式が存在することが見いだされ(モンストラス・ムーンシャイン:monstrous moonshine)、物理学の超弦理論によってこの問題が解決されている。
(参考文献)
涌井良幸,高校生からわかる複素解析,ベレ出版.
(例)アラン・マシスン・チューリング(Alan Mathison Turing,1912年6月23日 - 1954年6月7日)は化学反応の効果のみを考えれば安定的な空間的一様状態が拡散の効果が入ることで、そのコミュニケーション・リンク(およびそこで働く超偉大なるテンション(超万有引力!))による相乗効果によって不安定化しうることをシステムの安定性解析理論によって数学的に予見した(チューリング不安定)。拡散には平均化の作用があるため、拡散が加わることによって一様状態が崩れる(不安定化する)という現象は一見逆説的で奇異(きい)なことのように思われる。
チューリング不安定による複雑系生成メカニズムは1952年に『形態形成の化学的基礎』という彼が著(しる)した唯一(ゆいいつ)の生物学の論文として発表された。しかしながらそのコンセプトは生物学にとどまらず以後の非線形科学の分野に大きな影響を与える画期的なものであり、イリヤ・プリゴジン(Ilya Prigogine, 1917年1月25日 - 2003年5月28日)の『散逸構造(さんいつこうぞう)』や『自己組織化(じこそしきか)』の考え方(世界観)へとつながる重要なコミュニケーション・リンク(およびそこで働く超偉大なるテンション(超万有引力!))を有しており、自然界や社会の複雑な現象を解釈するうえできわめて重要な視点・世界観を与えてきている。
(参考文献)
齋藤正彦,長岡亮介,俣野博,松本幸夫,宮岡洋一,行列の解析学,東京図書,2017.
上記を踏まえてわれわれは、混沌(こんとん)の奥底に潜んでいる、ひとつながりの時間、空間、人-物間内の好循環の秩序(
自身にとっての真実の人生を全うするための骨格たる黄金のN角形ループ)をどうにかこうにか見出(みいだ)して、これを群知能(人間力の本質)によってうまくつなげて活用してゆくことにただひたすら注力(ちゅうりょく)すればよいのである!
Boys meets Girls ! 出会いこそ人生の宝探し!、
MisiaのEverythingの心持(こころも)ちである(フランク・ラムゼイ法)。
(注)
フランク・プランプトン・ラムゼイ(Frank Plumpton Ramsey, 1903年2月22日 - 1930年1月19日)は、イギリス・ケンブリッジ出身の数学者である。その生涯は非常に短かったが数学・哲学・経済学に大きく貢献したことで知られる。
(例) パスカルの法則は重要な漸化式(これもひとつのイノベーションにつながるコミュニケーション・リンク)で、パスカルの法則から二項係数および『パスカルの三角形』が生成できる(パスカルの法則は二項係数および『パスカルの三角形』の生成系になっている)。ここで、『パスカルの三角形』とは二項展開:
(n
k) xn−k yk (0 ≤ k ≤ n)
における二項係数:
(n
k)
を三角形状に並べたものである。
n ≥
k に対して


が成り立つ(パスカルの法則)。『n人からk人選ぶ組み合わせ』は『自分を含めてk人選ぶ組み合わせ』と『自分を含まずにk人選ぶ組み合わせ』の和に等しい。
(例)August Ferdinand Möbiusが1931年に発表したメビウス関数の定義を見ているだけでは一見、ゼータ関数との間にコミュニケーション・リンク(およびそこで働く超偉大なるテンション(超万有引力!))が存在するようには見えないがゼータ関数のオイラー積表現があるがために(なんと!)メビウス関数とゼータ関数との間のコミュニケーション・リンクを導くことができる。そうして、このコミュニケーション・リンク(およびそこで働く超偉大なるテンション(超万有引力!))のおかげで、リーマン予想と改良メルテンス予想とが同値であることを示すことができるのである。
(参考文献)木内 敬,ビジュアル リーマン予想,技術評論社,2020.
(参考文献)https://ja.wikipedia.org/wiki/%E3%83%A1%E3%83%93%E3%82%A6%E3%82%B9%E9%96%A2%E6%95%B0
メビウス関数は次のように定義される(ただし 1 は 0 個の素因数を持つと考える):
- μ(n) = 0 (n が平方因子を持つ(1以外の平方数で割り切れる)とき)
- μ(n) = (-1)k (n が相異なる k 個の素因数に分解されるとき)
- n が相異なる偶数個の素数の積ならば μ(n) = 1
- n が相異なる奇数個の素数の積ならば μ(n) = -1


(例)人類は最初に時間変動の少ない電磁気(学)の現象に気づいてしまったがゆえに、電界と磁界を別個の現象として捉えてしまい、永らく電界と磁界との間のコミュニケーション・リンク(およびそこで働く超偉大なるテンション(超万有引力!))に気づくことができなかった。
(参考文献)
竹内 薫,『ファインマン物理学』を読む,講談社.
(例)英単語の暗記作業で単語を最初に3つ覚えただけでは、その効果は全く感じられない。"I Love You !"と言うことがせいぜいである。しかしながら、英単語の暗記作業はあきらめずにこれを継続することで驚くべき効果を発揮し始める!英単語を1000個覚えると、その人がさらに3つ覚えるごとに英単語のコンビネーションの数は単純計算で600万以上増加する。
すなわち、学習を始めたばかりの時点では、その効果はほとんど感じられないが、これを継続してゆくことで、あるときふと、その学習(の複利的)効果が飛躍的に高まっていることに気づく。この事実はラムゼイの定理よろしく、すべての学問・研究活動においても同様に当てはまる。けっして途中であきらめてはならない(むしろ、あきらめることをあきらめなければならない)!漫画のワンピースよろしく最後の最後にすべての伏線が回収されればそれで良い(という学問・研究とよばれる複利のゲームをわれわれは戦っている)のだから、、、
(例)科学のどの進歩(progress)にも完璧な無知(ignorance)からはじまって、証拠(evidence)にもとづく部分的な知識が(超万有引力!的につながって)しだいに確実になるという段階を経て、事実上(in fact)確実になるという段階に至るという(複利的)変遷(transition)が含まれる(Howie)。
(例)2023年3月のWorld Baseball Classicは大谷翔平選手が投げた渾身(こんしん)のベスト・ピッチに呼応(こおう)して、エンゼルスの同僚のマイク・トラウト選手が渾身のベスト・スイングをするというシーンでクライマックスに達すると同時に熱狂(ねっきょう)の渦のなかで幕を閉じた。まるで映画のような筋書きに日本のみならず世界中が感動したが、そこにはマクスウェルの方程式において、あたかも内積と外積の協奏(きょうそう:Symphony)によって一筋(ひとすじ)の電気力線(電界)のまわりに円形の磁力線(磁界)が生じるのを眺めているかのような楽しさ、鍛錬されたもの達による力と力の協奏が産み出す超常(ちょうじょう:Paranormal)の美しさ(Beauty)があった。ボールが美しい円弧を描いてキャッチャーミットに吸い込まれた瞬間、実況アナウンサーは叫んだ、『Baseball wins !!!!(勝者は野球界だ!!!!)。』
(例)歴史(時間・空間・人-物間におけるコミュニケーション・リンクの本質・骨格・おおまかな流れ)を学ぶことはモノの観方・考え方・捉え方・発想の仕方・世界観を学ぶことであり、如何なる学問においても通用する、普遍・一般・抽象的に有効な(メタ的な)最強の学習方法(学問の王道)といえる。
具体的にたとえば数学を学ぶには数学史、科学を学ぶには科学史、語学を学ぶには語源を学ぶことによってそのつながり(コミュニケーション・リンク(およびそこで働く超偉大なるテンション(超万有引力!)))をまずは押さえることが、応用が利(き)きコストパフォーマンスに優れた直観的に見通しの良い学習方法と言える。
何事においてもそのつながり(の法則)をよくよく学んでおくことは抽出・分解・再構築(構造化、破壊的想像、イノベーション)力(にもとづく空間理解・把握力)をもたらす。つながり(の法則)を知っていさえすれば(TPOにあわせて臨機応変に)その場で単語の意味を抽出・分解・再構築(構造化)してその場の状況に対応することも可能である。
大規模言語処理(Large Language Model)においても、一連の文章を文節ごとに数値列(ベクトル)に置き換えて、そのつながりの確率を人工知能が学習することで、文章を再構築している。
英語の成り立ちとしてまずは5世紀ごろのゲルマン人の大移動によりケルト民族のブリトン人が使っていたケルト語とゲルマン語との邂逅(かいこう、出会い)によるコミュニケーション・リンク(およびそこで働く超偉大なるテンション(超万有引力!))から古英語が生まれた。
つぎに1066年のノルマン人による(グレートブリテン島南部の)征服(せいふく)により、古英語とラテン語(フランス語)との邂逅(かいこう、出会い)によるコミュニケーション・リンク(およびそこで働く超偉大なるテンション(超万有引力!))から中英語へと発展した(現代においてラテン語をもっとも忠実に継承している言語はスペイン語であるといわれている)。
それからもさまざまな言語との邂逅(かいこう、出会い)によるコミュニケーション・リンク(およびそこで働くテンション(超万有引力!))を経て、抽出・分解・再構築(再構造化)を繰り返し、洗練・進化して現在の英語に至っている。
(例)エミー・ネーターが研究を通じて道しるべとした行動原理は、つぎのようにまとめられるだろう。
『数や関数や演算どうしの関係性(つながり、コミュニケーション・リンク、そこで働く超偉大なるテンション(超万有引力!))を明瞭化して、統一(一貫)・統合(包括)的に適用できるようにし、その生産性を最大限に引き出すには、それを特定の対象から切り離して、普遍・一般・抽象的に有効な(メタ的な)概念として(再)表現しなおさなければならない。』
そうしてこのオブジェクト指向的な行動原理は、デジタル化ときわめて相性が良いのである!
(参考文献)
イアンスチュアート,数学の真理をつかんだ25人の天才たち,ダイヤモンド社.
(例)なにかあたらしい『モノ』を導入したくなったとき、既存の基本的な対象とそのあたらしい『モノ』との関係性に着目して、既存の対象の『集合』としてその『モノ』を構成するのがユリウス・ヴィルヘルム・リヒャルト・デデキント(1831-1916)の世界観であった。
デデキントの著書『数とは何かそして何であるべきか』の序文:
代数学や高等な解析学のかなたにあるようなものも含めて『命題のすべては自然数に関する命題に対応している』という世界観はディリクレから何度も聞かされたものであったが、上記のような世界観からは、これはまったく自明でなにも目新しいところもない主張であることがわかる。
しかし、この骨の折れる書き換えを実際におこない、自然数のみを扱うことにして、ほかはまったく認めないという(偏狭(へんきょう)な)態度は何の役にも立つものでもないように思われるし、ディリクレが言ったこととも(何(なん)ら!)関係がない。
逆に、数学やほかの科学での、最も大きく実り多い進歩は、むしろ、古い概念のみを用いたのでは表現が困難な複雑な現象が何度も訪れたところで、新しい概念(コンセプト)を創造して、それを導入することが余儀なくされたことによってもたらされたものである。
(参考文献)
渕野昌訳、数とは何かそして何であるべきか、ちくま学芸文庫.
藤田博司、『集合と位相』をなぜ学ぶのか、技術評論社.
眼の前の大波は 確かに高き波なれど いつか消えゆく波なれば
その奥底に潜む真実の 人生にこそ力注がん!
みなとみらいの波止場にて、Von Voyage !!!!
(サブ手段3)できるか?と問われたら(間髪いれずに自信満々の体(てい)で)、
『はい、もちろん(すくなくともトライしてみることは)できます!』とまずは(明るく、はきはきと)答えよう。そうしてそのあとで、つぎにどう実現するべきか(How)?その根拠は(Why)?を懸命になって考えるのだ(セオドア・ルーズベルト法)。
なぜなら、
だれもができっこないと思うことほど、(そのカウンターパンチとして)実際にやり遂げた時の価値がより一層高まるもの(つまり、
人々を感動させ、人生を輝かせる絶好のチャンス!!!!)であるからだ。
すなわち自身が主演している、『わが人生』というタイトルの檜(ひのき)舞台において、
全観衆があなたの一挙手一投足に対して注目し、『スタンディング・オベーション』をしている。そんな情景を(超行(運)動(道)計画図たるMe-DigIT Imaging vectorとして心に描き、)思い浮かべながら自分のなかにある、あらん限りの(先頭に立つ)覚悟と勇気、自己信頼感をもって『はい、もちろんできます!』と言い切るべきなのである!なぜならこのとき
相手はトライした結果できない可能性があるということを百も承知のうえで、その(先頭に立つ)覚悟と勇気、それから自己信頼感の有無(うむ)を問うているからだ。
『スタンディング・オベーション』は役者が舞台で輝くうえできわめて強力なマントラである。すなわち、『Make drama !』の名言で有名な長嶋茂雄監督が、ヒーローインタビューを受けている情景を(超行(運)動(道)計画図たるMe-DigIT Imaging vectorとして心に描き、)思い浮かべながら打席に立ったように、『スタンディング・オベーション』と心の中でつぶやきながら千両役者はたとえ小さな舞台においても全力で演技をするのである!!!!
すなわち、いま、この瞬間に自身が立脚する位置のまわりに一世一代の檜舞台(土俵・リング)が存在しているという物の観方・考え方・捉え方・発想の仕方・世界観である!
All the world's a stage and all the men and women merely players.
この世は舞台,人はみな役者(シェイクスピア)
さらに言えば、このマントラの効果によって勇気と自信を得ながらも、けっして高慢になることなく、周囲への感謝、リスペクトの気持ち、ならびに謙虚さを心の中で共存(きょうぞん)させておくことができれば百二十点満点、最高である!この『スタンディング・オベーション』のマントラは、ビジネス上の重要なプレゼンテーションにおいても絶大な効果があるので、ぜひ一度試されたい。
すなわち、
踊る阿呆に見る阿呆、同じ阿呆(あほ)なら踊らにゃ損々(徳島の阿波踊り歌のイントロ部)
の心持(こころも)ちである!(踊る阿法)
(重要なのは世界観だ!!!!)
さて、般若心経(はんにゃしんきょう)のなかに彼(か)の有名な『色即是空(しきそくぜくう)』という言葉がある。仏教の根本指導原理とされ、『すべての物事は突き進めて考えてゆくと実体が存在しなくなり、鍛錬・洗練された良質の世界観(神経というネットワークで有機的に繋がった目と手と脳、およびそこに、時としてあたかも神が宿るようにさえ見える、良質のモデル、型、枠)だけが残る(イデア論!)。そうしてそれらのモデル、型、枠は、sparseでありうる!すなわち、直観的(幾何学、野性的)に見通し良く単純・明解でありうる。』という考え方である。
(世の中の出来事や周囲の物事における)問題の本質(真髄・奥義・エッセンス)は原理・原則・定義・公理・機能・特(属)性・メカニズムおよびこれを基盤にして構築された全体を貫くモノの観方(鍛錬・洗練された良質の世界観)や考え方(コンセプト)、捉え方、発想の仕方の方にこそある。
単に表層(ひょうそう)の結果(実体)のみを(単体で)見たり、感情的になってただ闇雲(やみくも)に表層にある結果のみを追い求めるだけでは物事における問題の本質(超万有引力!的つながり)を把握し(つかみ)損ねることが多いということであろう。
本質は高周波ではなく、低周波成分にこそ現れるのである!そうしてそれらはsparseにmodelingされうる!すなわち、直観的(幾何学、野性的)に見通し良く単純・明解でありうる。
本質(モノの観方・考え方・捉え方・発想の仕方)は表面に顕(あらわ)れた結果から原因(へのつながり)を探索・推定し、原因(根幹にある基礎・基盤・土台・土俵(infrastructure))→結果(枝葉花(果)実としての応用)へのつながり(プロセス・根幹枝葉花(果)実)やその拡がりを時間軸、空間軸、さらには人-物間(じんぶつかん)軸をも踏まえて大局的につなげて観ることではじめて理解し、把握できるものだからだ。
つながれた本質はおそらく樹木の根幹枝葉花(果)実のような拡がりを持った、ひとつながりの有機的なネットワーク構造になっていることだろう。そうしてこのひとつながりの有機的なネットワーク構造を神経ネットワークで(超万有引力!的に)つながれた目と手と脳に普遍・一般・抽象化されたメタ的で柔軟なモデルとして展開し、これを有していることこそがわれわれの(発達する)知能そのものである!!!!。
表層に顕(あら)われた結果そのものが問題の本質そのものを体現するようなわかりやすい例もあるにはあるかもしれないが、複雑化する現実社会ではむしろ稀少(きしょう)であろう。
数学(や物理、そのほか、あらゆる自然科学)においても同様であろう。公式を鵜呑(うの)みにしてただ単に表層に顕(あら)われた結果のみを暗記するだけでは不足である。まず、その公式がなぜ(why)出てきたのか?公式が出てきた背景やその根本にある起点・原点・出発点(starting point)・一丁目一番地を探る。
つぎに、その公式の根本にある起点・原点・出発点(starting point)・一丁目一番地からどのような(how)指向性で、どのような(超万有引力!的)つながりをもって公式の根幹枝葉花(果)実(こんかんしようはなかじつ)が拡がり、存在しているのか?公式の骨格にあたる、プロセスをひとつながりにネットワーク構造として理解することこそが重要なのだ!
なぜならこのひとつながりの有機的なネットワーク構造としてのプロセスを神経ネットワークで(超万有引力!的に)つながれた目と手と脳にモデルとして展開し、これを有していることこそがわれわれの(発達する)知能そのものであるからだ。
想像力逞(たくま)しく、プロセスを補間・外挿しながら全体をひとつながりに(超万有引力!的に)つなげて観ようとするからこそ根本や背景に潜(ひそ)む問題の本質(全体を貫く原理・原則・定義・公理・機能・特(属)性・メカニズムおよびこれを基盤にして構築された良質のモデル・型・枠)に、ある時ふと、『なるほど!そういうことだったのか!(Eureka:ユーリカ)』と思い至ることができるのである(ユーリカ法)。
(例)科学のどの進歩(progress)にも完璧な無知(ignorance)からはじまって、証拠(evidence)にもとづく部分的な知識が(超万有引力!的につながって)しだいに確実になるという段階を経て、事実上(in fact)確実になるという段階に至るという(複利的)変遷(transition)が含まれる(Howie)。
(例)古代ギリシアの人々にとって多くの数学的概念は理想化されたプラトン主義の意味において『実在するモノ(モデル)』であった。プラトンのイデア論における最上位の現実とは抽象的な形態(概念)たる『イデア』レベルで『実在するモノ(モデル)』として(現代風にいえばサイバー/デジタルに)構成・ハンドリングされうる。
そうして、物質(理)的(フィジカル/アナログ)な世界は理想的な世界(イデア)の(モデルの)不完全な具現(象)化であるというモノの観方・考え方・捉え方・発想の仕方・世界観である。ここでプラトンの時代には存在しなかった『リーマンの写像定理』などによって代表される形態の柔軟性をある程度許容する位相幾何学とイデア論とは親和性がきわめて高く、プラトンの主義・主張を補強して拡大・普及・展開しうる可能性については留意が必要であろう。
(参考文献)イアン・スチュアート,川辺治之訳,無限,岩波科学ライブラリー,2018.
(例)満開の桜や華やかな紅葉といった美しいもの(表層に顕(あら)われた結果)を直接見るのではなく、補完(間)的想像力により(超解像度で!)観るほうがより本質的な(プラトンのイデア論における最上位の現実である、抽象(メタ)的な形態(概念)たるモデル・型・枠としての)美しさに肉薄し、これを味わうことができるという、中世の和歌や能楽にみられる『幽玄(ゆうげん)』と呼ばれるモノの観方・考え方・捉え方・発想の仕方・世界観。
『幽玄(ゆうげん)』という言葉は、囲碁のタイトル戦が行われる日本棋院の部屋の名称である『幽玄の間』にも使われている。囲碁においても『幽玄』と呼ばれる補完(間)的想像力による超解像度かつ抽象(メタ)的なモノの観方・考え方・捉え方・発想の仕方・世界観が極めて重要なのだろう(さあて、これから何を補完(間)しようか!?)。
 |
| 我が家の『幽玄の間』から見える右肩上がりの富士山。補完的想像力を掻き立てる。 |
(例)医療専門家は(超音波)診断画像上において目に見えない線を(超解像度で補間的に)引いて観ている。これに関連して、近年の深層学習技術を援用した超解像度技術の顕著な発達がある。具体的にたとえばDiffusion modelにおいては画像に対してあえてGaussian noiseを加えて、それを除去する方法をモデルが学習することによって画像の生成方法を学んでゆく。超解像度技術を用いることにより、低解像度の画像からAIが輪郭やテクスチャ(模様)がしっかり、くっきり、はっきりした高解像度の画像を想像して描くことができる。
低解像の生画像とそこから生成された超解像度の画像とを左右に並べてみると、何かしらインスパイアされるものがある。具体的な応用展開例としては超解像度の技術は低解像度のカクカクした線を高解像度でなめらかなものにしたり、領域を精確に抽出する際にきわめて有効であろう。さらに超解像度画像に基づいて、ターゲットに(イデア論的に)追従できれば、ロボットの(イデア論的な)動作のなめらかさや(イデア論的な)追従精度の向上につながるかもしれない。
イデア論よろしく、超解像度の技術はまた、低解像度の画像から抽象(メタ)的なモデルを分解・再構築するためにもきわめて有効であろう。ただし、実際の医用画像とAIが生成した超解像度の画像とを(医療従事者が実際の診断・治療に際して)混同してしまわないようにしっかり・くっきり・はっきりと区別して認識・ハンドリングできるように(その提示に際して)配慮しておくことは精確な医療を担保するうえできわめて重要なことであろう。他方で(イデア論的な)本質(的真実)は(部分的に)観測したものを普遍・一般・抽象化してメタ的に全体像を(補完して)分解・再構築することによって(はじめて)得られるべきものであることについてもわれわれは今一度、留意しておくべきであろう。
貧粗(ひんそ)・不足のなかに(で)こそ心の充足を見出しうるとする侘(わび)・寂(さび)の精神・心(こころ)とも通じうる(人生のどん底にあるときの心持(こころも)ちこそ決して忘れてはならないものの一つだろう。なぜなら、そのようなときの心持ちにこそ侘・寂の精神や心の充足が宿(やど)りうるからだ)。すなわち、物質的な充足と精神的な充足とは(あたかも正弦波と余弦波のような)相互に補完(間)的な関係にある(侘び寂び幽玄のこころ法)。
オイラーの公式
特に、θ = π のとき

となり、この関係はオイラーの恒等式(Euler's identity)と呼ばれる。
一般に区間[-π,π]上の関数f(x)を三角関数で展開するには、『正弦波』と『余弦波』の双方を合成することが必要である。これを関数f(x)のフーリエ級数展開という。
他方、区間[0,π]上の関数を三角関数で展開するには、『正弦波』あるいは『余弦波』の片方のみで展開できる。前者をフーリエ正弦級数展開、後者をフーリエ余弦級数展開という。どちらを用いるべきかは境界条件による。領域の境界線(面)に沿って未知関数がとるべき変数の勾配の値を与えるノイマン境界条件の場合は同じ境界条件(勾配~0~(-1)・sin(0):cosの微分)をみたすフーリエ余弦級数展開、領域の境界線(面)に沿って未知関数がとるべき変数の値を与えるディリクレ境界条件の場合は同じ境界条件(値~0~sin(0))をみたすフーリエ正弦級数展開を用いるのが好適である。また、両者のコンビネーションによるロビンソン境界条件というものもある。
(例)『正弦波』と『余弦波』はその黄金のコンビネーションによってあらゆる波動をその位相も含めて自在に作り出す(三角関数の合成公式、フーリエ級数展開を見よ!)。心臓(ポンプ)による血液の循環(脈動)も『正弦波』と『余弦波』の合成波による『正圧』と『負圧』の繰り返しである。あるお笑い芸人によれば人を引き付ける魅力的な話術の循環も『緊張』と『緩和』、『北風』と『太陽』、『押し』と『引き』の補完的な関係にある技の連続によってもたらされるという。地球を周回する月の引力によって引き起こされる潮の干満は地球に生命を吹き込むという偉大な役割を果たした。
人間の体は解剖学的に硬い骨(緊張)と柔軟な脂肪(緩和)そして(緊張と緩和の)双方向にわたって機能する筋・腱などによって構成されている。そうして超音波画像の適正化においても上記の解剖学を踏まえたうえで超音波プローブの『押し(緊張)』と『引き(緩和)』の絶妙な調整・制御がきわめて重要である。これについて詳細を知るためにはインピーダンス制御の理論を学ぶ必要がある。
秘する花を知ること。秘すれば花なり、秘せずば花なるべからずとなり。(世阿弥 『風姿花伝』)
AI(深層学習)がおこなっているのは、『読書百遍義自(どくしょひゃっぺんぎおの)ずから顕(あらわ)る』の(きわめて泥臭い!)戦略だ!たとえわからない(義において穴となる)一文があったとしても、一向(いっこう)に構うことはない!『秘するが花(秘することそのものが芸に最大の花を生む秘伝である)の風姿花伝』よろしく、そこで立ちすくむことなくいったん全体を読み切る(とことんまでやりきる)ことに集中したうえで、全体(の文脈)から部分(の地形、意味)を(推察、最大の花を咲かせるべく部分を)なんとか生成しようと苦心(くしん)すればそれでよいからだ。AIはうそをつくことも多いが同時にまた、『あたらずといえども遠からず』であることも多いからだ!
不自由を常と思えば不足なし
日光東照宮の陽明門(ようめいもん)の魔除けの逆柱(さかばしら)
1617年、江戸幕府の初代将軍・徳川家康(1543〜1616年)を祀(まつ)る神社として創建(そうけん)され、1636年に三代将軍家光によって造替(ぞうたい:reconstruction)された「日光東照宮」の社殿群(しゃでんぐん)のなかでもとりわけ目を引くのが日光東照宮の陽明門である。日光東照宮の陽明門は魔除けの逆柱でも有名である。
『建物は完成と同時に崩壊(ほうかい:collapse)が始まる』という伝承(でんしょう)を逆手にとり、わざと柱を未完成の状態にすることで災いをさけるという、言わば魔除けのために逆柱にしたのだという(すなわち、バランスを図ったのである!)。すべてが順調な瞬間(絶頂)こそが同時に最も危険な瞬間(滑落崖:かつらくへき)になっている可能性に留意されたい。2コイチセットでピンチはチャンス、チャンスはピンチ、登(のぼ)り坂は同時に降(くだ)り坂にもなりうるのだ!
未完成の建物と言えば、ガウディ(1852年6月25日 - 1926年6月10日)が設計したサグラダ・ファミリアが有名である。ガウディは柱と壁の傾斜を設計するうえで数字や方程式を一切使わず、10年の歳月をかけて実験を行ったという。その実験装置が日光東照宮陽明門の魔除けの逆柱よろしく、『フニクラ』と呼ばれる逆さ吊り模型であり、無数の紐(ひも)と錘(おもり)で構成されている。
網状の糸に重りを数個取り付け、その網の描く形態を上下反転したものが、(再急降下の(曲線状の斜面をもつ)滑り台と(自転車のタイヤ上の1点が軌跡として描く)サイクロイド曲線の上下反転関係よろしく!)垂直加重に対する自然で(なおかつ美しい!)丈夫な構造形態だと、ガウディは考えたのだという。建設中に『建物が崩れるのでは?』と不安がる職人たちに対して、ガウディは自ら足場を取り除き、構造の安全性を実証して見せたという。
強なくして用なし、用なくして美なし、美なくして建築ではない!
ウィトルウィルス(2000年前のローマの建築家)が建築十書において
実際につながっているかどうかはここでは問題ではない。『仮想接続』ともゆうべき仮想的なつながりの(コミュニケーション・リンク(およびそこで働く超偉大なるテンション(超万有引力!))が貼られた)状態をまずは設定してみて、そこで相互に働くであろう作用(力やモーメントなど)や化学融合反応などを想像力たくましくあれこれと仮想してみることこそが重要なのだ!(仮想接続法)
すなわち、
ドラえもんの歌の冒頭で『こんなこといいな、できたらいいな♪』と夢に描いてあれこれと仮想する、あの考え方である。
これは、以下の4つと類似(similar, analogous)の考え方である。1つ目は関数の連続性を証明したいがために、『その関数はつながっていないのではないですか?』と訴える原告の存在を仮想して、訴えられた被告の弁護人としての立場からε-δ/ε-N論法などをもちいて、『いやいやこの関数は確かにつながっていますよ!』と原告の主張を真っ向から否定してこれを退けることで弁証法(べんしょうほう)的に関数の連続性について確認することである。嘘(うそ)をつけばそこから必ず矛盾が生じるのだ。
(参考)弁証法(背理法)と対偶(たいぐう)法の関係についてわかりやすくまとめられている。いずれも結論(B)をまずは否定するところから出発して前提(A)の矛盾(あるいは否定)をみちびく。
①は実数の数直線テープをはさみでカットすると、いずれか片方(こちらが閉集合となる)にのみ境界点が付属して、その点はもう片方(こちらは開集合となる)のいずれの点よりも境界が属する閉集合側に位置するだろうという世界観。②は無限遠点に位置している実数にむかって有理数の列が延々脈々累々と(ぐるぐる巻きに!)小数点以下の桁数をふやしながら伸びてゆく世界観である。
上記と類似(analogous)するものとして線路の先に(極限たる節目(ふしめ)の集積(しゅうせき)点として!)ある無限遠点や無限遠直線(水平線)などは透視(とうし)図法などを用いて絵画にも描かれ、われわれの目で実際に確認(視認:しにん)できるものである(あるいは現実の風景に重ねてイメージすることができるものである)が、これは射影幾何学的世界観においてはユークリッド平面外の点やその集合として捉えることができる。射影幾何学においては平行線はユークリッド平面外の無限遠点において交わるのだ!
上記の無限遠点の可視化はわれわれが順序数を(0:空集合が対応する→ 空即是色),1,2,3,…,ω,ω+1,ω+2…と自然数による可算無限(ω)を超えてもなお、さらにそこから仕切(しき)り直して数え続ける※ことができる※※(可算無限を超えたその先もこれまた可算になっている!)という、超限(ちょうげん)順序数の存在を信じるに足る、直観(・幾何学・野性)的な根拠を与える。
※『数え続けることができる』というよりは『順序づけることができるかどうかのチェック』といったほうが直観的にはしっくりくるかもしれない、、、(なぜなら数えあげるという物理的なタスクで物事を捉えてしまうと古代ギリシャのソフィストたちがハマったアキレスと亀のパラドックスという(きわめて心理学的な!認識の)罠(わな)に陥(おちい)ってしまう危険性があるからだ。現実的な問題として自然数による可算無限(ω)までを数えている間にヒトの一生は(はかなくも!)おわってしまうことだろう、、、真剣に数えはじめてしまえば最後、われわれの命はいくつあっても足りなくなるだろう、、、(とどうしても思ってしまい、きわめて心理学的な認識の罠に陥(おちい)ってしまう、、、))。そうであるならばむしろ(心機一転、逆転の発想!一撃必殺の返し技で)、可算というよりは(レールの敷板の)可配置(かはいち)性のチェックといったほうが幾分(いくぶん)かはよさそうだ。これならば少なくとも数えあげるという物理的なタスクからわれわれは解放される(ため、その(あくまで)数学的な実在(じつざい)性を(心理学的に!)しっかり・くっきり・はっきりと実感することができよう)、、、
透視図法によって描かれた線路の2本の平行線が無限遠点で交わっていることによって超限(極限)順序数を具体的にイメージとして捉えたうえで、さらに有限の時間のなかでアキレスが亀に追いつき、追い越すことができ、追いつくまでの(数学的!)距離空間はイデア論的に順序数としての自然数によって(物理的にではなく、あくまで数学的に!)無限に分割し続けることができる(かどうかのチェック)という、古代ギリシャのソフィストたちが論じたアキレスと亀の逸話を想起(そうき)すればより具体的で直観的な超限(極限)順序数のイメージが得られるであろう(われわれの物理的世界では物理的距離空間の分割においてプランク定数にもとづく制約が生じるが、数学的概念としては上記の距離空間の順序数としての自然数による分割は可能(自由自在)であるとして矛盾が生じない。リーマンの写像定理よろしく、ありとあらゆる、対(つい)となる正則(せいそく)な領域の間には位相幾何学的に1対1の対応がついてしまうからだ)。すなわち、(物理的にではなく、あくまで)数学的実在である!。
(参考文献)
横山明日希,数式図鑑,講談社.
プラトンのイデア論よろしく、『現実の物理的世界は理想的な数学的モデルの不完全な具現化である』と捉えよう。理論として矛盾さえ生じていなければ数学的にはそのモデルの実在が許される。数学的実在は物理的な制約の問題とは無関係である。
すなわち、カントールが発案した後述する実無限(じつむげん)のモノの観方・考え方・捉え方・発想の仕方、世界観を援用することで線路の敷板(しきいた)の敷設(ふせつ)作業は集積点(極限点)たる無限遠点までの区間を(ω個の要素からなる)ひとかたまりのブロックとしていったん敷設作業に節目(ふしめ)の区切りをつけた後、そこ(無限遠点たる集積点)からさらに(あるいは仕切り直して節目の前後で線路の敷板につける順序数の付番(ふばん)をひっくり返すこともなく、その順序の整合性を維持したまま(ω+1)として)一から敷設し始めることができる(すなわち、集積点たる節目までを(ω個の要素からなる)ひとかたまりのブロックとして捉えて(ω個の要素からなる)ブロックをブロック単位で順番に敷設してゆこうという世界観である!)!
ここで、可能無限(かのうむげん)であっても実無限(じつむげん)であっても、0(あるいは1)から自然数の枠を超えて超えて限りなく、そして果てしなく無限にならんだ何かであるという点においては相(そう)が入らず、いずれも(超限)順序数と呼ばれている『自然数の一般化』として捉えることができる。
しかしながら心理学的には両者は区別されている点には留意(りゅうい)が必要である。すなわち、可能無限では、常に有限個の自然数を数えあげた状態をその都度(つど)プロセスとして考え、自然数の集合の要素の個数は、数え上げるというプロセスを繰り返すことを通じてどんどんどんどん、いくらでも積み増しながら増やしてゆける(そうして、このような作業プロセスは延々脈々累々と(ぐるぐる巻きに!)繰り返すこともできる!のだから、その先のプロセスを考えることなど一見、われわれにとっては全くもって意味がない、無駄なことであるかのような『むなしい』思い(『心理的な限界』)に囚われる!)※、動的に変化する個数であるという世界観で捉えている。
※数学はその対象(たとえばスタティックな対象としての無限たる実無限)とプロセス(たとえばダイナミックなプロセスとしての無限たる可能無限)のいずれにおいても概念的なものである。他方、心理学的にはこれらは区別されている。しかしながら数学的によくよく考えてみると、これらは同じ硬貨の表裏(ひょうり)であって矛盾なく相並立(あいへいりつ)しうる概念であるということがわかる。
すなわち、プラトンのイデア論よろしく概念的なモノであるという点においては両者の間に相(そう)は入らず、いずれの概念も数学的世界観としてその存在が許される(したがってTPOにあわせて2つの世界観を都合よく使い分ければよく、もちろん実無限のなかに、可能無限のプロセスを組み込むなど、『世界観(視点)を切り替えながらの心理的な限界突破!』という一撃必殺の返し技で両者を併用するという大胆な世界観も許されうる!)。
無限のページをめくった(極限値を与えるωの)その先からまた、あらたな節や章を設けて、ω+1ページ目という起点を設定、延々・脈々・累々と(ぐるぐる巻きに!)ページを順序づけてゆくことは数学的モデルとして実在可能である(理論として矛盾さえ生じていなければ数学的にはそのモデルの実在が許される)!ワイエルシュトラスのε-N論法よろしく、極限操作においてはいつでも後だしジャンケンで勝てるということのみを確認(check)して、無限のその先に歩(ほ)を進めたとしても一向に構わない(矛盾は生じない)のである!
他方、実無限では、自然数の集合の要素の個数は、最初から可算無限個(ω)がすでに存在している(前述の無限遠点の可視化(とアキレスが有限時間内に無限のプロセスを経て亀を追い越すこと)!が百聞は一見に如かずでその視覚的な根拠を与えている!)のであり、(動的に変化しない!)静的なひとかたまりの(コンクリートの!)ブロックであると捉える(最初から無限個を数えあげられているものとして(ω個の要素からなる)ひとかたまりのブロックとして(前述の無限遠点たる集積点は透視図において1点に定まることを直観的根拠にして!)スタティックなものとして取り扱うことにする)。
2つ目はロボットを構成するひとつながりの、ひとつひとつのリンクについてその運動方程式を立てたいがために仮想仕事の原理で無限小変位なるものを仮想して(まずは弱形式で)遠心力を含めた力やモーメント(を書き出してみてそ)の釣り合い状態を考えることである。
3つ目は棒や板状の物体の変位・変形状態を知りたいがためにその軸に沿って、軸に垂直な仮想横断面を設定して、いくつかの(あるいはその極限として連続的な状態を解析するために無限個の)パーツに分けたのちに、仮想横断面における相互作用(作用・反作用)や、ひとつひとつのパーツに働いて、その結果パーツに変形をもたらす(上記仮想横断面に作用する内力としての)力やモーメントの状態について考えることである。
4つ目は複素関数論に出てくる、解析接続の考え方。漸化式の構造をうまく活用して数学のプロの柔軟な世界観によって定義域をすこしづつずらしながら何度も関数を再定義してゆくことでガンマ関数やリーマンのゼータ関数の定義域(土俵)はどんどん負の領域へと広げてゆくことができる。
ガンマ関数の定義:

部分積分を巧妙に用いた下記の漸化式によって解析接続してゆくことでガンマ関数の定義域(土俵)はどんどん負の領域へと拡大してゆくことが可能である。
![{\displaystyle {\begin{aligned}\Gamma (z+1)&=\int _{t=0}^{\infty }{t^{z}(-e^{-t})'}\,dt\\&=\left[-t^{z}e^{-t}\right]_{t=0}^{\infty }+z\int _{t=0}^{\infty }{t^{z-1}e^{-t}}\,dt\\&=z\Gamma (z)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ca0d996dec7a0da6e85ba7cf1a22fa352c71760)
と定義される関数をベータ関数と呼ぶ。ベータ関数は、次のようにガンマ関数と結び付き、組み合わせ関数の自然数から実数への拡張になっていることがわかる。

リーマンのゼータ関数とは、

で表される関数のことである。上記のガンマ関数を用いれば、リーマンのゼータ関数を

と再定義することもできる。
さて般若心経(はんにゃしんきょう)の『色即是空(しきそくぜくう)』は、
色、即是、空(しき、そくぜ、くう、色→空)とよむ
このあとさらに、
空、即是、色(くう、そくぜ、しき、空→色)
とつづく。
『色』は(自己、他者、ならびに周囲の環境が相互に作用、影響を及ぼしあい、押しくらまんじゅうしながら構成する)世界(の景『色』)、『空』は(中身を『空』の状態にしたフレームとしての)世界観(神経というネットワークで有機的に繋がれた目と手と脳およびそこに宿るモデル・型・枠)をあらわし、
良質な(自己、他者、ならびに周囲の環境が相互作用しながら構成する)世界が良質な世界観(良質のモデル、型、枠)を育(はぐく)み、良質な世界観が良質なシステム(モノゴト)を産み出す。また、これを通して良質な世界をつくる。
この良質な世界がさらに良質な世界観を生み出す、、、(読書百遍(百万遍)!奇跡をもたらすこのサイクルの繰り返し)、、、
上記の正の連環(れんかん)がプロセスとして何度も繰り返されると、良質な世界観はさらに変化・変容しながら鍛錬・洗練、収斂(しゅうれん)進化してゆき、時にあたかも神が宿るようにさえ感ぜられる良質のモデル・型・枠を産み出(析出)したり、その根本や背景にあり、全体を貫く原理・原則・定義・公理・機能・特(属)性・メカニズムおよびそのつながりや拡がりを深く理解し、これに精通することへとつながってゆく。
ということであろう。
(仮説)AIと人間は同じ(データ)環境(地図)を与えられると収斂(しゅうれん)進化する
(例)砂漠の一粒一粒という構成要素が集まることによって、サハラ砂漠やアラビア砂漠といった特徴的な全体(の構造)が構築されているという集合論的なモノの観方とアラビア砂漠における砂粒と砂粒の間の関係性や(全体の)構造(互いに他を磨きつづけている)が一つ一つの砂粒に役割(や輝き)を与え、その砂粒を特徴づけているという構造論からの2方向からの観方があり、2つの観方は相(あい)並立しうる。
(例)アニメ『鋼の錬金術師』では「一は全、全は一」とは何かと師匠から問いかけられたアルとエドが無人島に放り込まれ、そこでサバイバルするなかで万物(ばんぶつ)の流転(るてん)を体感(たいかん)し、世界の真理の断片(だんぺん)を見出した。
(師匠からの問い)一は全、全は一(One is ALL, ALL is One)とは?
(アルとエドの回答)全は世界、一はオレ(ALL is the WORLD, One is Me)
(例)要素が関係性や(社会)構造をつくる、あるいは関係性や(社会)構造が要素に役割を与えるという具合に、因果関係は互いに逆方向に働いていることに着目されたい。水や空気が流れることによって創り出される紋様(もんよう)であり、錬磨(れんま)された、一粒一粒がその構成要素となっている美しい砂紋(さもん、Ripple marks)は自然が創り出した絶景であるが、その裏には上記の双方向性が働いていることに気づく。我々一人一人と社会との関係も似たようなものかもしれない。ちなみに砂紋(さもん)がそのまま化石となったものは漣痕(れんこん)と呼ばれる。
(参考文献)
柳谷 晃,天才数学者たちの超・発想法,大和書房.
藤田博司,集合と位相,技術評論社.
菊池 誠,公理という考え方,数学セミナー,Vol.71, No.8, 2022.
(しなやかで柔らかいモデルとトポロジー)~~~~~~~
ここでいう、モデル(型・枠)とは原理・原則・定義・公理・機能・特(属)性・メカニズムにもとづき、(印加されるエネルギー)によって中国の伝奇小説『西遊記』に登場する如意金箍棒(にょいきんこぼう)よろしく柔軟に形を変えうる言わば、『しなやかさをもった柔らかいモデル(型・枠)』であることが好適である。
なぜなら、しなやかなモデルは、周囲の環境との間で特異(特徴)点を考慮しつつ適切な美しい均衡・バランス状態をうまい具合(ポジティブかつゴキゲン)につくり出し、系に印加されるエネルギー変化(状況変化)に応じて臨機応変に形状(境界)を変化させながら、周囲の環境とうまく相互作用するからだ。
如意金箍棒(にょいきんこぼう)の最大の大きさは上が三十三天(忉(とう)利天)、下は陳莫(地獄の最下層で18層目)にまでに達する(伸縮柔軟性を有している!)と伝えられている。ここで如意金箍棒は固有(関数)ベクトル(空間)そのものであり、その大きさを変化させるものはその固有(関数)ベクトル(空間)が有している固有値である(ここで(パルス)伝達関数の極(システムの固有方程式の根、特異点、Me-DigIT HARVEST)とその状態空間表現のシステム行列の固有値とは一致して、たがいに等しいことに留意(りゅうい)されたい)。ビッグバン以降、光の速度(秒速30万km)でわれわれの住む宇宙は膨張(ぼうちょう)しつづけているというが、如意金箍棒の直観的イメージはまさにそのようなもの(固有ベクトル空間の固有値に応じた膨張(空間をこじ開けてゆく)作用)であろう。
制御理論によれば、(パルス)伝達関数の極(システムの固有方程式の根、特異点、Me-DigIT HARVEST)とその状態空間表現のシステム行列の固有値とは一致して、たがいに等しい(特異点(システムの伝達関数の極、システム行列の固有値、システムの固有方程式の根、Me-DigIT HARVEST)あるところに固有モード(固有値・固有ベクトル)あり(虎穴に入らずんば虎子を得ず)!、古典制御理論における極(特異点、Me-DigIT HARVEST)と現代制御理論における固有値(システムの固有方程式の根、固有ベクトル:固有モード)とをつなぐ超偉大なる黄金のコミュニケーション・リンク(時空人間を超越した超偉大なる超張力、言わば『超万有引力!』))。
柳に雪折れなし、しなやかな柳の枝は、風雪に耐えて折れること(singularity)がないという。対して、堅い木は雪の重みに耐えかねて枝が折れることがあるそうだ(しなやか柳法)。
上善如水(じょうぜんみずのごとし、老子)
水のようにさまざまに変容(変位・変形・回転)する柔軟性を有し、他者と争わず、自然に流れるように生きるのが人間(じんかん)においても理想的な生き方であるというモノの観方・考え方・捉え方・発想の仕方・世界観。
柔よく剛を制す(老子)
柔らかいモデルを扱うのはゴム膜に描かれた図形よろしく、『三角形』も『四角形』もあるいは『円』も閉曲線として同じものだと捉えるトポロジー(位相幾何学)という学問である。トポロジーとエネルギーの概念をうまく組み合わせて、硬直化しているモデルをしなやかさをもった柔軟なものにできないだろうか?と動力学的な世界観から捉えなおして考えてみることは有効であろう。柔らかいモデル(柔軟な幾何学)の有用性について理解するためには複素関数論のコーシーの積分定理や留数定理についてより深く学ぶことが有効であろう。
しなやかで柔軟なモデルにおいては相互作用によって力が均衡・バランスするところに境界ができ、印加されるエネルギーにもとづいてモデルの形状(境界)は動的に変化する。
(例)曲がった空間のなかで曲がらずに(曲率ゼロで)直進する測地線の概念がある。
(例)『コ』も『く』も『L』も『z』も同じものだとみなす感覚が『位相幾何学』の世界観である。すなわち、これらの間に『相(境界線)』を入れない。
(例)『三角形』も『四角形』もあるいは『円』も同じものだとみなす感覚が『位相幾何学』の世界観である。すなわち、これらの間に『相(境界線)』を入れない。
(例)『立方体』も『四面体』もあるいは『球』も同じものだとみなす感覚が『位相幾何学』の世界観である。すなわち、これらの間に『相(境界線)』を入れない。
(参考)
都筑卓司、トポロジー入門、講談社.
~~~~~~~(しなやかで柔らかいモデルとトポロジー)
動揺(どうよう/ゆるぎ)のない『明鏡止水の世界観』を以て、いま現実に目の前で起こっている世の中の出来事や周囲の物事を(時間的・空間的・人-物間的にまたがって存在する)ある全体の出来事や物事の一部分として補間しながらそのつながりや拡がり(としての本質)の全体を俯瞰(ふかん)して捉えようと(空間の全貌(ぜんぼう)・全体像を理解・把握しようと)する、言わば『視野連結拡大型の大局(俯瞰)的な世界観』で粘り強く取組むからこそ(実装)解へと到達できる問題があることを知るべきである。
時間(歴史観)、空間(世界観)、人-物間(人-物観・人生観・哲学・動力学はじめ、あらゆる自然科学)!およびそれらの間に働く超偉大なる超万有引力!!!!(千野俊猛先生)
時間、空間、人、物の間をつなげてモノゴトを大局(俯瞰)的に観よう!そうすることで、これまで観えなかったモノゴトの本質を新たに一連のつながりとしてその拡がりとともに浮かびあがらせることができ、これを捉えてイノベーションにつなげてゆくこともできよう。
すべての出来事や物事はほかの出来事や物事と通じている(通じてゆける)、網目のように有機的につながっている(つなげてゆける)、連関している(連関してゆける)と、時間的、空間的、さらには人-物間(じんぶつかん)的に大局的な目で柔軟に捉え、想像力逞しく考えるべきである(蜘蛛の巣法)。
(例)どの産業がどれくらいの付加価値額を生み出しているのかを把握できると、日本あるいは世界経済に対する解像度がぐっと高まる。1936年にワシリー・ワシーリエヴィチ・レオンチェフは経済効果の指標として今日も国や地方自治体などで汎用的に用いられている産業連関(れんかん)表をもちいた分析手法を提案した(レオンチェフの産業連関表)。第二次世界大戦後の経済予測に際して、産業連関分析は他の分析方法と比較して、非常に高い精度を示したことから、その有用性と重要性が広く認められるようになった。
産業連関表をタテ方向に読めば、それぞれの産業間の会計的なつながりが推察できる。またヨコ方向に読めば、それぞれの産業とお客さんとのつながりが見えてくる。産業間にコミュニケーション・リンク(およびそこで働く超偉大なるテンション(超万有引力!))が張られていることを直観的に実感できる表と言えよう。
(参考)
(例)1940年代にP.H.レスリーは年齢構造を考慮した人口動態モデルを提唱した(レスリーの人口動態モデル)。
You have to trust that the dots will somehow connect in your future. (Paul Steven Jobs, この点と点とが兎にも角にも将来むすびつくという(時空人間を超越した超万有引力の存在に対する揺(ゆ)るがぬ)信念をもたなければならないのです。)
ここで、点というのは、点の集合(点群)たる領域のニュアンスで捉えられるべきであろう。点の(連続無限の!)集合たる領域(線分の距離、図形の面積、立体の体積)と領域とが結びついた世界をまずは自身の頭のなかにイメージとして描き、つぎにこれを具現化してゆくのである。ウォルト・ディズニーはディズニーランドが完成するまえになくなったが、すでに頭のなかにはディズニーランドが明確に構築されていたのだという。
また、自分の生まれ育った家はすでに各自の頭のなかで明確にモデル化されているので、取り壊された後になってもずっとモデルとして頭の中に(生きている限り!)存在していると言えるのである。
すなわち、今現在、あなたの頭の中にある、過去・現在・未来のさまざまなモデルは、今この瞬間にでもあなたの頭のなかで時空を飛び越えて随意(自由自在、at will)に結びつけることができるのだ!未来はあなたの頭の中にすでにモデルとして現在において実際に存在して(しまって)いるのだ!!!!
とても重要なことなのであえてもう一度言おう、
未来はあなたの頭の中にモデル(プラトン風に言えば、最上位の現実たるイデア(概念))としてすでに現在において実際に存在して(しまって)いるのだ!!!!(このことは我々がけっしてネガティブな思考に陥ってはならない理由でもある)。想像力をフルに発揮して、頭のなかでモノゴトを極力ポジティブに結び付けることを心がけよう!!!!
われわれが目指すべきは時間・空間・人-物間のなかにコミュニケーション・リンク(およびそこで働く超偉大なるテンション(超万有引力!))を貼ってゆくことでポジティブな黄金のN角形ループをただひたすら追求し、これを構築してゆくことだ!!!!Imagine Positively!!!!
すべての道はローマに通じており、すべての血管は心臓につながっているのである!すなわち世界中どこにいても、意志あるものにはだれにでも、富士山やエベレストの頂(いただき)に到達する道が開けているのである!そうしてこれこそが『(真の)自由(自在、随意、at will)とは何か?』という人類の永遠のテーマに対するひとつの答えでもある!
All roads lead to Rome.
All blood vessels lead to the heart.
(無数の毛細血管の存在が血液が全身を隈(くま)なくめぐる行動の自由を担保している。大企業と中小企業の関係も同様であろう。単なる生産性の問題などでは決してない!)
Where there's a will(人生を全うするための固有値),
there's a way(人生を全うするための固有(関数)ベクトル(空間)).
— Abraham Lincoln (1809 - 1865)
“If you build an army of 100 lions and their leader is a dog, in any fight, the lions will die like a dog. But if you build an army of 100 dogs and their leader is a lion, all dogs will fight as a lion.”
— Napoleon (1769 - 1821)
Exercise makes excellence, excellence makes
freedom(訓練で洗練され、洗練されると自由を得る)。このセンテンスは修練が単なるスキルの習得ではなく、それ以上の内的自由の獲得につながることを表現しています。(橋詰博行先生)
『自由と平等』は社会の理想の姿(イデア論的なモデル)として望ましいとされることが多いが、平等な社会の(フィジカルな)実現は原理的に不可能である。なぜなら、ひとりひとりの起点・原点・出発点は本質的に異なるものだからだ(生まれる国・地域・家庭・生まれ持った各自に固有の遺伝子やその発現としての身体特性(超固有値および超固有ベクトル:超固有モード)などはいずれも選択できないものばかりである)。
そうして、そうあるからこそわれわれの属する社会には多様性が確保されているのだと言うこともできる。すなわち、もし平等な社会をどうしても実現しようとすれば、われわれは(群知能に大いなる向上をもたらす)社会の(すばらしい)多様性を放棄せねばならなくなるだろう。
しかしながら、上記の意味での自由な(開かれた)社会の実現は平等社会に比(ひ)してある程度までは現実的に達成可能である。時間・空間・人-物間上を(道や血管のように)ひとつなぎにすることで、意志さえあれば(苦労をいとわなければ)誰もがそこに到達できる(人生レベルで可到達(かとうたつ)である!)という意味での自由な(開かれた)社会の実現はわれわれにとって現実的かつ合理的な目標といえる。
そうしてこの自由な(開かれた)社会を実現するために重要なのは群知能(ぐんちのう)という考え方をわれわれ一人一人が持つことであろう。つまり、『私は』という局所のみを観る視点・視座(しざ)を一刻もはやく脱却して、『われわれは』という全体を俯瞰(ふかん)して観ることができる、言わば『大我(たいが)』の視点・視座で生きるのである!(大我法)
(例)有向(ゆうこう)グラフにおいて矢印をたどって任意の頂点から任意の頂点へと移動できる(すべての頂点が行き来できるという意味でつながっている)ことを強連結(きょうれんけつ)という。これについてより詳細を知るためには(規約)ルート系の理論について学ぶ必要がある。
(例)つながっていないと思えても、(実は)つながっている!と捉えうる世界観が重要である!コミュニケーション・リンク(およびそこで働く超偉大なるテンション(超万有引力!))の張られていないWEBページどうしは、(皮相的にみれば)つながっていないと考えるのが一般的で自然な捉え方なのかもしれない。しかしながらこれをランダム・アクセス・リンクを含めてあらためて捉えなおせば、(実は)つながっていると捉えうる(あるいは相手に捉えさせる)世界観も可能になってくる。そうしてこうした世界観をうまく活用してゆくことで、より統一・統合・普遍的な(強運・強者のメタ的な)思考や群知能(ぐんちのう)構成が可能になってくるのである。
(例)線分の両端を無限の彼方(かなた)まで伸ばした直線(あるいは開曲線)は、その両端が無限の彼方でつながっている(すなわち曲率半径∞の円弧)と捉える世界観においては、正円(あるいは閉曲線)と一対一の対応がついてしまう。すなわちこのような世界観のもとでは正円(あるいは閉曲線)と直線(あるいは開曲線)の間に相は入らない。
これについてより詳細を知るためには、角度を保存しながら直線/正円を直線/正円に写す共形(あるいはその二つ名を等角ともいう)写像の理論やn次元双曲幾何学のモデルであり、その幾何学のもとでの各点が n次元円板あるいは球体に属し、かつその幾何学のもとでの直線がその円板に含まれる円板の境界と直交する円弧または直径によって与えられる有名なポアンカレの円板について学ぶ必要がある。
コミュニケーション・リンク(およびそこで働く超偉大なるテンション(超万有引力!))の数が増えると、それだけ拘束条件が増えるのだから、これに囚(とら)われて一見不自由になってしまうのではないかと感じられるかもしれない。しかしながらこのような認識は弱運(じゃくうん)・弱者の捉え方である。コミュニケーション・リンクの数が増えれば、それだけ取りうる選択肢の数が指数関数的に増大するのだから、その分自由になれると捉えるのがより統一・統合・普遍的な強運・強者のメタ的な思考法である。すなわち、より多くの橋(Golden Me-DigIT Gate Bridge)をかけること(connecting dots)でより自由に行き来ができるという強運・強者の世界観である。
そうして、これに応じてできることの数も増大してゆく。時間・空間・人-物間に有効なコミュニケーション・リンク(およびそこで働く時空人間を超越する超偉大なるテンション(超万有引力!))を貼ってひとつなぎにしてゆくことこそが真の自由(自在)を獲得するための黄金の道(Golden Me-DigIT Road)である! (時間・空間・人-物間に有効なコミュニケーション・リンク(およびそこで働くテンション(超万有引力!))を貼ってゆく法)
最終目的地さえ見失わなければ、いつかあのMe-DigIT Mountainの頂にも到達することができる、そういう感覚をもっていることが重要かつ素敵ですね!
Exercise makes excellence, excellence makes
freedom(訓練で洗練され、洗練されると自由を得る)。このセンテンスは修練が単なるスキルの習得ではなく、それ以上の内的自由の獲得につながることを表現しています。(橋詰博行先生)
おほぞらに そびえてみゆる 高嶺にも 登れば登る 道はありけり
(明治天皇)
(特に物理学と比較したときの)数学の本質はまさにその(発想の)自由さにこそある
Georg Ferdinand Ludwig Philipp Cantor(1845-1918)
・・・しかしこれとは異なった路、すなわち与えられた集合に距離を導入することなしに公理的な手段によって(開円板と同相な)開集合(あるいは閉集合であってもよい)を再定義するという路をたどることもできる。
この路(みち)はきわめて大きな行動の自由を保証するもので、この路をたどれば位相空間(トポロジー)という(あらたなる)概念に至(いた)る。
A.N.Kolmogorov (1903-1987) and S.V.Fomin (1917-1975)
Aus dem Paradies, das Cantor uns geschaffen, soll uns niemand vertreiben koennen.
カントールが我々のために創造してくれた楽園から、誰も我々を追い出すことはできない
David Hilbert(1862-1943)
カントールの楽園とは、カントールの創造した『実無限の世界』であり、具体的には無限(を数の)集合(の仲間として土俵にあげ、これをハンドリングするための方法)論のことである。『カントールの創造した楽園をけっして離してはなるものか!』というのがヒルベルトの当時の心持(こころも)ちであったと伝えられている。
ここで、実無限(無限に対応する数)が実際にこの世界に存在するかどうかを考えることはさして重要ではない(すくなくとも数学的な世界観モデルとしては概念(イデア)レベルでこの世の中に実在している!と言い切れる)。そのような世界観(モデル)をまずは持ってみてあれこれと推論を展開してみることこそが有効で、本質的かつ決定的に重要なのである!。
楽園から追放されたくない一心のヒルベルトは、集合論の矛盾を追放すべく、仲間や弟子と共に研究を続けた(ヒルベルト・プログラム)。時は流れて1931年、ゲーデルの不完全性定理がヒルベルト・プログラムに一つの否定的な結論を降すことになる(オッペンハイマーはこの結果を『ゲーデルは人間の理性の限界を示した』と評した。この事実をどう受け止めるかは人それぞれの世界観によるだろうが、
たとえ否定的な結論が得られたとしてもそれは悲しむべきことではない!むしろこれを契機(けいき)として生かして世界観を大転回する起点・原点・出発点とするべきである!一切は心に従って転ずる!!!!)。このときヒルベルトは70歳であった。
この考え方により、問題を解決に導くための情報量を飛躍的に増やしてゆくことが可能になり、問題の根本や背景にひっそりと隠れている、全体を貫く既知/新規の原理・原則・定義・公理・機能・特(属)性・メカニズムおよびこれを基盤にして構築された良質のモデル・型・枠を見出したり、これを随意(自由自在、at will)に活用することが可能になる(これはあらゆるモノとモノとをつなげる技術であるIoTがもつ底知れない破壊的イノベーション効果とも通じていよう)。モノ(ヒト)とモノ(ヒト)とがつながること自体に効果(価値)があるのだ。一方で、インターネットにつながっていないスマートフォンやPCの魅力は半減してしまうのだ、、、
『視野連結拡大型の大局的な世界観』を持ち、(動揺のない)明鏡止水(めいきょうしすい)の世界観(
よく磨かれた鏡(よく鍛錬し、よく洗練された者)は水の動態をもよく捉えうる(空間の全貌(ぜんぼう)・全体像をよくよく理解・把握しうる)分解能(プロの観察眼・世界観)を有するということであろう)を以て、プロセスと結果を照らし合わせながら、WhyやHow(5W1H)を納得できる形になるまで、あきらめずに(あきらめることをあきらめて)とことん突き進み、深堀り調査・研究して粘り強く考えぬく!
このことによってできうる限り本質(真髄・奥義・エッセンス)に迫らんとする、この姿勢こそが研究開発者がまず第一にもっておくべき矜持(きょうじ)と心得るべきであろう。
偉人は(折れることのない如意金箍棒がごとき一本の心の槍を有しながらみずからの人生に固有のシャンゼリゼ大通り(固有(関数)ベクトル空間)を)突き進んでいるからこそ偉人たりえるのだ!!!!
艱難(かんなん)汝(なんじ)を玉にす。
Adversity makes a man wise.
千日をもって『鍛』とし、万日をもって『錬』とする。
磨くその 力によりて 瓦とも 玉ともなるは 心なりけり。
(石川 理紀之助(りきのすけ))
ボールが止まって見えた。川上哲治
ボールが止まって見えたのは、まさに明鏡止水のごとく鍛錬の結晶として、『打撃の神様(プロ)の世界観』が洗練された良質のモデル・型・枠として川上哲治元巨人軍監督の頭の中にあたかも神が宿ったかのように構築されたからであろう。
(5W1Hによる思考展開)~~~~~~~
思考展開の基盤(本質)は、社会がたとえどれだけ進化したとしても、未来永劫これまでと同様に5W1Hとともにあるだろう。
Why ? How ?(世界観)
When ?(時間)Where ?(空間)
Who ? What ?(人-物間)
今後、AI・IoT・ロボット技術の進展にともない、Who(人)とWhat(物)がどんどんつながりを持ちはじめて、その境界についてはどんどんフワッと(Who-What)あいまい化してゆくことだろう(
ヒトとモノをつなげて同相のものとしてフワッと柔軟に捉える(トポロジカル的な)モノの観方・考え方・発想の仕方・世界観、言わば『フワッと(Who-What)思考』が今後ますます重要になりそうだ、、、)。
~~~~~~~(5W1Hによる思考展開)
なぜ(Why)、そのように(How)発想して効を奏して問題解決に至ったのか?原理・原則・定義・公理・機能・特(属)性・メカニズムおよびこれを基盤にして構築された良質のモデル・型・枠として全体を貫くモノの観方(世界観)や考え方(概念やコンセプト)(これこそが出来事や物事における問題の本質をなすもので、ほかの問題に対しても応用が効き、横串としてグサグサ突き刺さる、真に学ぶに値するべきものであろう)は何なのか?をとことん突き進め、深堀りして粘り強く考えぬくことこそが最重要である。
縦のつながりのみならず、横のつながりを構築・強化する(横串を入れる)ことが重要(横串法)。なぜなら(ネットワークよろしく)縦横につながることは縦横への随意(自由自在、at will)な展開を可能にするからである。
松本洋一郎先生
東京で言えば、山手線、京浜東北線、ならびに中央線、大阪でいうと環状線と御堂筋線は人-物の流れにおいて本質的であろう。
別の観方をすると、どんな研究開発対象であっても、深掘りして粘り強く研究開発していさえすれば、全体を貫くモノの観方(世界観)や考え方(概念やコンセプト)に通じてゆくことができるのだ!
そうして(鍛錬・洗練の結果として)これによく通じたプロの世界観を構築していることこそがプロジェクトを先導・けん引する立場にある研究開発者に期待されていることであり、研究開発プロジェクトのリーダー(あるいはマネージャー)があたらしいプロジェクトを立ち上げるうえで求められる必須の要件であり、博士号が『博士(○○学)』とよばれるゆえんであろう(○○はどんな研究開発対象であってもよく、自らの人生を全うするための固有(関数)ベクトル空間たる専門分野(人生を全うするためのシャンゼリゼ大通り)を極めんと決して縮退することのない不滅の熱意(1以上の固有値)をもって突き進むことが、博(ひろ)く識(し)ることにつながるのだ!)。
“If you build an army of 100 lions and their leader is a dog, in any fight, the lions will die like a dog. But if you build an army of 100 dogs and their leader is a lion, all dogs will fight as a lion.”
— Napoleon (1769 - 1821)
ここで、上記の全体を貫くモノの観方(世界観)や考え方(概念やコンセプト)に通じることは、別の捉え方をすると、随意(自由自在、at will)であることを求める活動でもあり、面白きこともなき(この浮(憂き))世をとことんおもしろくする活動でもある!ことを指摘しておく。
Exercise makes excellence, excellence makes
freedom(訓練で洗練され、洗練されると自由を得る)。このセンテンスは修練が単なるスキルの習得ではなく、それ以上の内的自由の獲得につながることを表現しています。(橋詰博行先生)
時には固い岩盤に突き当たって縦に進めなくなり、横展開してまわり込むことを余儀なくされることもあろう。他方で地表から新たに掘り始める回数はできるだけ最小限に抑えたい。
なぜなら人ひとりに与えられた時間には残念ながら今のところリミットがあるからだ(若い時節にはあまり感じられなかったことだが、人生も折り返し地点に差しかかると否応(いやおう)なく時間のリミットを痛感させられることになる、、、)。
逆に言うとリミットを強く意識するからこそ、自分自身の人生の最終目的地にむけて自らがやらずにはおられない(自分にとっての真実の人生につながる)タスク(自分にとっての人生を全うするための本質、骨格)を見出してこれを設定、あらん限りのパワーのフォーカスをそこに加えて力強く骨太に、自分自身にとっての真に実のあるかけがえのない人生を辿(たど)り、突き進んでゆくことができるのだともいえる。
今、顕在化(けんざいか)して目に映っている出来事や物事(点)を、時間的・空間的・人-物間(じんぶつかん)的にまたがって存在する、ある全体(線分、図形、立体)の一部分として大局的に捉えうる視野連結拡大型のよく鍛錬され、よく磨かれた(明鏡止水の)プロの世界観をもつことが、(リーダーとして)問題を解決に導いたり、物事を好転させるうえで本質的かつ決定的に重要である。
結果は水面上に現れた氷山の一角に過ぎず、水面下にあるもの(プロセス)をふくめた全体を補間・内挿(ときには外挿)してつなげてみなければ出来事や物事の本質を見誤る。すなわち(リーダーとして)真佛(真実、本質)を観ることが出来ていないということになる。抽象化の階段を何段かのぼり、さらには具体(現)化の階段を何段か下ったところに真佛(真実、本質)が潜んでいたというケース(事例)は(個人あるいは世界の)歴史を紐解けば枚挙にいとまがないのだ。
“If you build an army of 100 lions and their leader is a dog, in any fight, the lions will die like a dog. But if you build an army of 100 dogs and their leader is a lion, all dogs will fight as a lion.”
— Napoleon (1769 - 1821)
(仏教の世界観)~~~~~~~
諸行無常(母校の東大寺学園の転心殿(てんしんでん)中央に線刻されている。
生滅(しょうめつ)の法は苦であるとされているが、生滅するから苦なのではない。生滅する存在であるにもかかわらず、それを常住(じょうじゅう)なものであると観るから苦が生じうるのである。この点を忘れてはならないとするのが仏教の主要な世界観のひとつ。
https://ja.wikipedia.org/wiki/%E8%AB%B8%E8%A1%8C%E7%84%A1%E5%B8%B8
東大寺学園
この世に安住の地はありません(橋詰博行先生)
人生について(安住の地を目指す)脱出ゲーム的な捉え方(世界観)も可能かもしれないが安住の地は(すくなくとも現世においては)なさそうだ、、、。他方で安住の地などないからこそ、これを尊いものと捉えることもできよう。これを踏まえて人生の荒波(あらなみ)の中においてこそ心(精神)を(不完全ながらもなんとか少しでも)安住(安定化)させてゆこうとする心持ち(気構え)こそが(きわめて)重要になってくるのであろう、、、
かつて学園が東大寺の境内(けいだい)にあった時、毎日登下校の際、大佛殿本尊(だいぶつでんほんぞん)の毘盧遮那佛(びるしゃなぶつ、いわゆる大仏さまのことである。『毘盧舎那』とはサンスクリット語の『ヴァイローチャナ』の音訳で太陽の意味。)に礼拝するのがならわしになっていた。
その心を生かすべく、転心殿が造(つく)られたのだという。これは今思い返してみても大変良いならわしであったとおもう。なぜなら大仏様や
不動明王(ふどうみょうおう)、太陽、富士山、雄大な自然、北極星、そういった偉大なものからパワーをいただいて、偉大なものによって自分自身が生かされているのだと信じることは安全・安心・安定的で
( Me-DigIT 魂のこもった!)思いやりのあるハンドリングにつながり、精神衛生上大変よい効果をもたらすからだ(負けの9割は他人に負けているのではなく、自分自身に負けているという。精神衛生の安定の確保はかくも重要である!)。
大仏さまはお釈迦様の身長を10倍することで『時間・空間・人間(じんかん)を超越(通貫)する存在であるこの宇宙(世界)そのもの』を表現しているともいわれている(まさに如意金箍棒(にょいきんこぼう)そのものである!)。
東大寺の大仏を建立した、聖武(しょうむ)天皇は華厳経(けごんきょう)の考え方を政治に取り入れ、人々の心が( Me-DigIT 魂のこもった!)思いやりの精神でつながれるようにするための政策をさまざま講じたといわれている。
すべては神(さまざまなプロの多様な世界観!まさに八百万(やおよろず)の神々!)の恵み(のおかげ)である!!!!(マルティン・ルター)
Stay Hungry, Stay Foolish, and Stay Wild, first and foremost !
さて、今一度、諸行無常という仏教用語について考えてみよう。この仏教用語はこの世の現実存在(森羅万象:しんらばんしょう)はすべて、姿も本質も常に流動変化するものであり、一瞬といえども存在は同一性(identity)を保持することができないと説くものであった。ここで世の中がこうあることに気付いてしまったことは決して悲しむべきことなどではない!ことには留意(りゅうい)が必要であろう。むしろこの状況を生かしてみずからのモノの観方・考え方・捉え方・発想の仕方・世界観を大転回する契機(チャンス)と捉えるべきなのである!一切は心に従って転ずる!!!!
諸行無常の言葉のごとく、時代は変化・変容し、周囲の状況は時々刻々と変幻(へんげん)するものであるが、変幻する世の中にあるからこそ、(時間の経過に随伴・付随して世の中に印加される、大小様々な変換操作に対して)位置が不動なものや方向性(姿勢)を変えない(不動の)もの(固有(関数)ベクトル空間)は大変ありがたく尊いのだ!そうしてそれらはわれわれが人生を生きてゆくうえでの重要な羅針盤(らしんばん)になりうるものなのである。
静中動(せいちゅうどう)あり、動中静(どうちゅうせい)あり
(例)俳句に『色変えぬ松』という絶妙な季語がある。周囲の木々が紅葉し、色を変えてゆく(変調してゆく)なかで松だけは変わらない。このことを利用して、変わりゆく周囲のなかで変わらないものが変わらず、ありがたく存在しつづけているというコントラスト映像を描写することによって季節の変化を捉えようというきわめて巧妙な手法である。すなわち、変わらないものが変わらず、ありがたく存在しつづけていることによって周囲の変化をより際立たせて精緻に捉えることができるというのである!
(例)時代の変革期には(複素平面上に置かれた)社会システムに不可逆な回転のモーメントが加わり、実業(複素平面の実軸)と虚業(複素平面の虚軸)が少しづつ入れ変わってゆく。これを踏まえて研究開発では現在は虚業だけど将来は実業になってゆくだろう(半歩先の)ものを積極的に狙ってゆくのがよいであろう。
なぜならこれらは(人間にとっての見通しのよさや扱いやすさへの探求から発展した、ツールとしての)線形代数学でいうところの、なんらかの変換操作に対する不動点(位置が不動、北極星)や固有(関数)ベクトル空間(姿勢や方向性が不動)に相当するものであるからである。
これら不動で、直観的で扱いやすく、なるべくシンプルなものから、人生を全うするためのバックボーン、船でいうところの竜骨(りゅうこつ)をうまく構成してゆければ、時に複雑怪奇で鬼ばかりが存在しているようにさえみえる、渡る世間(せけん)においても、すこしは人生の見通しを良くすることができるのではないだろうか。たとえ屈曲(くっきょく)している世界(外界)の中にあっても(自身の固有(関数)ベクトル空間(内界)のなかで)真っ直ぐ進むことができる測地線が必ず存在していることに留意するべきであろう。
(例)上流から下流にむかって(マクロ的にみて)一見したところ、真っすぐ進む、直進する大河の流れであっても、川の中心軸付近と川岸付近とではその進行速度には差(勾配:こうばい)があり、(ミクロの視点でみれば)この速度差が局所的には回転する流れ(渦流:うずりゅう)をつくり出し、水面に浮かんだ木の葉をクルクルと回転させてしまうのである!
(例)ジョン・フォン・ノイマンが提案したZF(ツェルメロ・フレンケルの)集合論における正則(せいそく)性の公理(こうり)の意味は、おおよそ以下のような背景から生まれたものである。
(背景)ラッセルはカントールのP(V)(集合全体の集合)がもたらす矛盾を解析して、核となる部分を抽出した。これをラッセルのパラドックスという。ラッセルのパラドックスは集合概念の一体全体どこが矛盾をつくる原因になっているのかをきわめて明解なものとした。これによって集合論が本当の意味で深刻な危機に陥っているということが誰の目にも顕(あら)わなものとなった。
『それ自身を要素として含まない集合』を『M集合』とし、『すべてのM集合を成分とする集合R』を作ってみる。そうすると、『任意の集合X』に関しては、『XはRに含まれる』⇄『XはXに含まれない』という定式が成り立つ。そして特にX=Rとすれば、『RはRに含まれる』⇄『RはRに含まれない』となり、パラドックスが明示される。
『この矛盾を解消するべくわれわれは空集合0から出発して、その集合、その集合というふうに0から順々に生成したものだけを集合の仲間として扱うこととし、どこかわけのわからないところから突然まぎれ込んだ(どこの馬の骨ともわからない)ようなものをわれわれは集合とは扱わないことにする。』
任意の性質 P(x) に対して、P(x) を満たす元 x の集合 {x|P(x)} が存在する。しかしながら、内包公理からは、上述のとおり、以下が構成でき、パラドックスが発生する。

したがって、集合論の公理は通常の数学を集合論の上で展開するために十分なだけの集合の存在を保証しつつ、パラドックスを発生させる集合は構成できないように慎重に設定する必要がある。
(参考文献)竹内外史,集合とはなにか,講談社,2001.
(時間の経過に随伴・付随して世の中に印加される、大小様々な変換操作に対して)時々刻々と変化・変容する、複雑怪奇に見える日常世界のなかにいるからこそ、上記のような(位置、姿勢、方向性が)不動なものをありがたいモノとして目にしたり、思い浮かべたりすることが精神衛生を良好に保つうえで、きわめて有効なのである。
これら不動なものは周囲が変化すればするほどより大きな存在感を示すため、おのずとその空間における特徴点や特異点を形成することとなる。
われわれ個人個人の(人生を全うするための)固有値、固有(関数)ベクトル(空間)こそが我々の多様性に富んだこの豊かな世界の特徴点や特異点を形成する根本・源泉となっていることに留意されたい
私も出勤日にはできうるかぎり、職場の
電気通信大学のとなりにある
布多天(ふだてん)神社にお参りすることを日課にしている。なぜなら
布多天神社にゆくと日々の運動ポテンシャル・エネルギー(ラグランジアン)が注入(ちゅうにゅう)・充填(じゅうてん)され、高まるような気がするからだ。ハミルトニアンは運動エネルギーとポテンシャル・エネルギーをあわせた全エネルギーだが、ポテンシャル・エネルギーの減少分が運動エネルギーへと転化(てんか)する(運動エネルギーとポテンシャル・エネルギーとは正弦波と余弦波のごとく相互に補完的な関係にある)ことを考慮すれば運動の原動エネルギーたる運動ポテンシャル・エネルギーは運動エネルギーと(ー1)×(ポテンシャル・エネルギー)の和になる。
{\displaystyle H=H(q,p;t)\,=T+V}
{\displaystyle L(q,{\dot {q}},t)=T-V}
{\displaystyle {\frac {\partial L}{\partial q_{i}}}(q(t),{\dot {q}}(t),t)-{\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {q}}_{i}}}(q(t),{\dot {q}}(t),t)\right)=0}
さらに、人生の最終目的地たる未来の一点をクリアに心に描いて、そこからパワーをもらい、そこにアトラクトされるという考え方を持つことも同様にオススメである。なぜなら人生を全(まっと)うするためのバックボーン、船でいうところの竜骨(の姿勢・方向性)を一定に維持する効果が期待できるからだ。
人生のパワースポットにはもうひとつあり、それは自分の時間・空間・人-物間の起点・原点・出発点(starting point)・一丁目一番地であろう。わたしも昔からの友人や先輩、恩師、小学校、昔住んでいた家の近所のおばさんからパワーをいただいている。
Dionne Warwick - That's What Friends Are For
人間困ってしまえば開き直って何とかなるものだ。開き直るには原点(自身の人生を全うするために固有の中立軸、人生を全うするためのシャンゼリゼ大通り)に立ち帰るのが一番(まずはシャンゼリゼ大通りに立ち帰って、われわれにポテンシャルエネルギーを供給する燦燦と輝く太陽の光を思う存分、浴びてみよう!)。(保江邦夫)
上記の3つのパワースポットを手に入れることができれば、あとは極力、強く、しなやかで、陽気(
ポジティブかつゴキゲン)な人生を生ききることに注力(ちゅうりょく)するだけでよい。その準備は整っているし、もはや何も迷うことはなく、ただ不惑(ふわく)の人生を突き進むのみだ!
自身の人生の起点・原点・出発点・一丁目一番地・starting point・基礎・基盤・土台・土俵・infrastructure・根本・根幹枝葉花(果)実・目標・目的・マイルストーン・最終目的地・経由地をうまく(あるいは曲がりなりにでも)定義できれば自身の人生を全(まっと)うするための骨格、船でいえば竜骨(りゅうこつ)の設計図が出来あがる。
そうすれば、自身の人生を全(まっと)うするための固有値・固有(関数)ベクトルもおのずと定まり、心の中に折れることのない一本の槍を宿すことになる。これによりあなたの人生の第二幕(The second act of your life)が開くはずだ!あとはこの心の中に宿る折れることのない一本の槍をもって自身の人生を全(まっと)うするために燦燦(さんさん)と輝く太陽の光を思う存分味わいながら、自身の人生に固有のシャンゼリゼ大通り(固有(関数)ベクトル空間)をまっすぐ突き進むことにただひたすら注力(ちゅうりょく)するのみである!
偉人(リーダー)は心の中に折れることのない一本の槍を宿して、自身の人生に固有のシャンゼリゼ大通りを突き進んでいるからこそ偉人(リーダー)たりえるのだ!
さて転心殿に向かって左側には、転心殿の名前の由来であり、『華厳(けごん)経』の最も大事な核心部分である如心偈(にょしんげ)の中の一節、『一切従心転(一切は心に従って転ずる)』などの言葉が線刻されている。
あらゆる価値観や感性(モノの観方、世界観)は、その人の心の持ちようによって、いろんなものに(topologicalに!)変現しうる。これに気づいた時、その人は(自身に固有の人生を全うするための)真佛(真実、本質)を観ることが出来ると説(と)いている。
いかなる状況にあっても(たとえ暴風雨のなかにおいてさえも!)重心低く、ブレることのない自身の人生に固有の軸を見出し、あらん限りのパワーをその軸(自身の人生に固有のベクトル空間)に印加(input)し続けてこそ(自身に固有な(関数)ベクトル空間において)真佛(真実、本質)を映し出す明鏡止水(めいきょうしすい)のプロの世界観が構築され、その結果としてはじめてヒトは(自分自身にとっての)真実(本質)の人生に迫り、これを辿(たど)り、突き進むことができるのだ!
何事においても(人生においても!)その本質・骨格は低周波成分にこそ顕(あらわ)れる、すなわち単純・明解でありうることに留意(りゅうい)するべきである(重心低く、ブレてはならない!)。すなわち、天命(destiny)を受け入れてあらたな人生の第二幕(The second act of your life)を切り開き、これを境(さかい)に面白きこともなき(この浮(憂き))世がどんどん、どんどん面白くなってゆくのである。
具体的に、人生を全(まっと)うするための軸や世界観はひとりひとり異なるものであるが、時間・空間・人-物間における(人生の)起点・原点・出発点(starting point)・一丁目一番地と(人生の)最終目的地とが(初期条件あるいは境界条件として)与えられれば、おのずから、自分にとっての人生を全(まっと)うするためのシャンゼリゼ大通りたる人生を全(まっと)うするための軸が一意に定まり、結果として人生レベルでの自分自身に固有の価値・評価基準も一意に定まる。言わば『心に宿すべき折れることのない一本の槍』が定まる。
この軸を人生を全(まっと)うするための中立軸たるバックボーン(本質、フレーム)に据えて極力ブレない(時間の経過に随伴・付随して印加されるさまざまな変換操作に対して中長期にわたって姿勢を変えない、固有(関数)ベクトルの)ように(なるべく線形に!)制御(中長期的にみれば、バックボーンや幹、線路のごとく軸は時間軸に沿ってしなやかに変化・変容・洗練・進化してゆくこともあろうがその場合においても新幹線(や大河の流れ)よろしく、線路(中立軸線)の曲率はなるべく小さくなるように抑えて慣性力(運動ポテンシャル・エネルギー)を極力落とさずに維持)しながら突き進むのである。たとえ屈曲している世界の中においても真っ直ぐ進むことができる測地線が必ず存在しているのだ。
川の流れのように(美空ひばり)
なぜなら人生を全(まっと)うするための軸を(さまざまな変換に対する固有(関数)ベクトルとして!)しっかりと確立し、これを固定することができず、周囲の意見によって人生を全(まっと)うするための軸をコロコロと変えてしまうようでは、人生を全(まっと)うするための骨格(人格)がまだ十分にできているとは言えず、そのような人についていってしまうと、精神的にも肉体的にも慣性力(運動ポテンシャル・エネルギー)を損耗してしまう(もちろん当の本人も疲労・困憊(こんぱい)・損耗してボロボロになってしまう)からである。背骨がゴムのようにぶよぶよだと、人は歩くことさえ困難であろうし、家の柱が細くて十分な剛性が得られなければ、地震のたびに生命の危険にさらされ、不安な思いをすることになるだろう。
そしてそのような人は中長期的にみて周囲の信頼を得ることがきわめて困難になってしまうのである(つまり、リーダーとしては不適ということになる)。なぜなら、いつ意見を変えてしまうかわからない人を中長期的に信じきることはまったくもって、きわめて困難であるからである。われわれは何事においても(もちろん人生を全うするうえにおいても!)その本質・骨格が低周波成分にこそ顕(あらわ)れる、そうしてその本質・骨格に沿って進むのが最善であることを経験的に知っている!
“If you build an army of 100 lions and their leader is a dog, in any fight, the lions will die like a dog. But if you build an army of 100 dogs and their leader is a lion, all dogs will fight as a lion.”
— Napoleon (1769 - 1821)
本質は高周波ではなく、低周波成分にこそ現れるのである!そうしてそれらはsparseにmodelingされうる!すなわち、直観的(幾何学、野性的)に見通し良く単純・明解でありうる。
他方、
自分自身の人生を全(まっと)うするための軸(すなわち、心の中に宿す、折れることのない一本の槍、船でゆうところの竜骨)をしっかりと固定できれば、他人の世界観(軸)が投影された助言・助力のなかからも、これを(内積をとるなどして)評価して真に必要な成分だけを抽出、自分自身の人生を全(まっと)うするための軸に(正)射影して、(力のモーメントとして)ありがたく頂きながら、周囲と協調しながらも自身の人生を全(まっと)うするために固有の最終目的地に向かう推進力へとうまく転換してゆくことができるのである。一切は心に従って転ずる!
相手の助言・助力を最大限に活用するということは、相手の助言・助力をただ単に鵜呑(うの)みにするということでは決してないことには注意が必要である。すなわち相手の助言・助力を(内積をとるなどして)評価して真に必要な成分だけを抽出、自分自身の人生を全(まっと)うするための軸に(正)射影して、(力のモーメントとして)ありがたく頂いてこそ相手の助言・助力を(推進力として)最大限に活用することができているといえるのである。これが相手の助言・助力を受けるときの最大限の礼儀・敬意である。
他人の意見(を自分軸で評価することもせずにただ単に鵜呑(うの)みにすること)で(生命の神髄(クイントエッセンス)にもとづく)自分のほんとうの心の声(自分軸)を消してはならない
(Steve Jobs)
そうしてそのような人は中長期的にみて周囲からの信頼を勝ちとることができるのである(つまり、リーダーとして好適であるということになる)。なぜなら、時間の経過に随伴・付随して印加されるさまざまな変換操作に対して中長期にわたって不動(不動点)な人(-物)や、評価軸(固有(関数)ベクトル)をしっかり有していてこれを簡単に変えない人(-物)は、人生を全(まっと)うするための骨格(フレーム)を設計するうえで、その構成要素として直観(幾何学)的に将来の見通しがよく単純・明解(快)で、安全・安心・安定的に
( Me-DigIT 魂のこもった!)思いやりをもってハンドリングでき、計算に入れることができる人(-物)であるからである。いわゆる『人(-物)生を全(まっと)うするための(骨格)筋(きん)が一本通った、変節することのない筋(すじ)の良い人(-物)』と評価されうるのである。人生レベルにおいて一本の筋(すじ)を通すことはかくも重要なのだ!
“If you build an army of 100 lions and their leader is a dog, in any fight, the lions will die like a dog. But if you build an army of 100 dogs and their leader is a lion, all dogs will fight as a lion.”
— Napoleon (1769 - 1821)
人生を全(まっと)うするための(最大)固有値という重き荷(慣性の大きな、
重い心の
槍)を背負えば足腰(体幹)も強くなり、重心も自ずと低くなり、運動もむだが少なく鈍感で低周波なものにならざるを得ない。このことが(人生を全(まっと)うするための固有(関数)ベクトル空間がしっかりと定まった足腰の強い)変節のない人生へと導き、他人に対する
( Me-DigIT 魂のこもった!)思いやりにもつながるのである。
また、通常ほとんどの人は、目先の成功・失敗(勝敗)に惑(まど)わされて、一喜一憂(いっきいちゆう)してしまうものだが、目先の成功・失敗(勝敗)に惑わされるものは、自らの可能性(才能、将来)の芽(め)を摘(つ)んでしまう人である。1000年後に残る大聖堂を建てようと中長期的視野で未来を見据えれば、時には小事をのみこんで(失敗も受け入れて)、目をつぶること(忍耐)も必要になってくる。成功に漕ぎつけるまでに1000回失敗することを覚悟するべきであろう。
すなわち、『諸行無常』の言葉のごとくこの世の現実存在(森羅万象:しんらばんしょう)はすべて、姿も本質も常に流動変化するものであり、一瞬といえども存在は同一性(identity)を保持することができないからこそ不動点や固有(関数)ベクトル空間はありがたく、『色変えぬ松』のごとく、環境のなかでそのひとを特徴づける、複素積分でいうところの特異点(singularity point)としての役割を果たし、これをみずからの心の中に宿し内包することによってこそ、その人の魅力・存在感はより一層高まりうるのである!
素人は特異点を扱いが困難で得体の知れないものとして、忌避(きひ)しがちな傾向にあるが、(数学の)プロは扱いが困難で得体の知れない特異点の付近でこそ、なにがしか重要な手がかりが隠れていやしないかと刮目(かつもく)してよくよく調べようとするという。組織や社会においてもこれは同様である。特異点を(生み出す人生を全うするための固有値および固有(関数)ベクトル空間を)有するとんがった人材の内包とその有効活用こそが魅力的な組織や社会を構築するうえできわめて重要なのである!(『色変えぬ松』法)
具体的にたとえば部品のサプライヤーであれば時間軸上の中長期にわたって、以前の部品との互換性を維持しつつ、一定品質以上の部品をブレのない製品開発の設計思想(プロの世界観)のもとで『安定供給しつづけることが信頼につながる』のであり、企業としての軸(骨格)がブレずにしっかりしているといえる。さらに部品の性能がすこしづつでも上記の設計思想のもとで向上しつづけていればいう事なしである!
すなわち、人生の最終目的地と起点・原点・出発点(starting point)・一丁目一番地から導出される人生を全(まっと)うするための航路からのずれに対して慣性(質量)・粘性・剛性を適正に制御するのである!時間の経過に随伴(ずいはん)・付随(ふずい)して印加されるさまざまな変換操作に対して中長期にわたって不動(不動点)な人(-物)や、評価軸(固有(関数)ベクトル)を変えない人(-物)はある程度の慣性(質量)・粘性・剛性を感じさせ、変節することのない頼れる、( Me-DigIT 魂のこもった!)思いやり(重い槍)のある人(-物)といえよう!
本質は高周波ではなく、低周波成分にこそ現れるのである!そうしてそれらはsparseにmodelingされうる!すなわち、直観的(幾何学、野性的)に見通し良く単純・明解でありうる。
人の一生は重荷(慣性、搭載荷重:ペイロード)を負うて(最終目的地を明確に抱き、意志を集中・集積させて)遠き道を行くがごとし。急ぐべからず。
重き荷(重い心の槍)を背負えば足腰(体幹)も強くなり、重心も自ずと低くなり、運動もむだが少なく鈍感で低周波なものにならざるを得ない。このことが変節のない人生へと導き、他人に対する( Me-DigIT 魂のこもった!)思いやりにもつながるのである。
不自由を常と思えば不足なし(拘束条件の存在を一々気にするな!)。
こころに望みおこらば困窮したる時を思い出すべし(さまざまな外部環境による拘束・作用を受けても、インピーダンス:慣性・粘性・剛性を適正化してこれに柔軟に対応せよ)。
堪忍(インピーダンス:慣性・粘性・剛性を適正化して柔軟に対応すること)は無事長久(ぶじちょうきゅう)の基(もとい)、いかりは敵と思え。
1週間以上続くような怒りは稀(まれ)である。換言すれば、われわれが感じる怒りの多くは人生を全(まっと)うするための本質とは全く無関係である。このような怒りによってわれわれのエネルギーの多くを無駄に消費するべきではない。怒りを感じたときには、これに捉われることなくなるべくすみやかに人生を全(まっと)うするための本質部分にフォーカスを移すように心がけるべきであろう。怒り・恨みの情動は決して学習・記憶するべきものではない!なぜならこれらは苦痛に変化してしまい自らを一生苦しめてしまいかねないものであるからだ。
眼の前の大波は 確かに高き波なれど いつか消えゆく波なれば
その奥底に潜む真実の 人生にこそ力注がん!
慣性・粘性・剛性はしつこい汚れのごとく、除去することは困難である。むしろこれを活用する道(うまい返し技、一撃必殺のカウンターパンチ)を考えよう。
勝つ事ばかり知りて、負くること知らざれば害その身にいたる(最適な道よりもむしろ、知的なフィードバック(鍛錬・洗練)が多様に得られる周辺の多様な道を多様に歩もう!そうすることで失敗(の構造)をプロセスとして学ぼう(機序・構造論研究にこそ価値がある!))。
おのれを責めて人をせむるな(作用反作用の法則を知れ!)。
及ばざるは過ぎたるよりまされり(エネルギー効率の観点から行き過ぎ量:オーバーシュートを極力避けるように制御するべきである)。すなわち、資源・エネルギーの有効活用である。オーバーシュートは感染症のパンデミックにおいてもそうであるが、システムの崩壊へとつながってしまう、、、そうしてオーバーシュートを避けるためには重き荷(重い心の槍)を背負うこと、すなわち( Me-DigIT 魂のこもった!)思いやり(重い槍)が有効かつ重要ということであろう、、、
(例)動力学の観点からは、出発点と初速だけが与えられた質点が外力なしで歩む曲面上の軌跡を測地線(そくちせん)とよぶ。すなわち、測地線とは曲がった空間の上で曲がっていない曲線(曲面のなかの人から見ればこれは直線に見える)のことであり、曲面上の最短経路は測地線となる(逆は必ずしも言えない)。三角不等式よろしく無駄に曲がれば道のりは増えるのだ!
これとは逆の発想(世界観)で、曲がっていない空間にあえて(ユークリッドの平行線の公理を満たさないという意味での)曲がった空間(たとえば双曲空間)を(たとえば双曲計量を導入することで)導入し、空間を再設定し直すこともできる。ただし、双曲空間は人間が直観・幾何学・野性的に捉えるには複雑すぎることには注意されたい(このため近年まで数学者にさえ認識されてこなかった)。
これはシンプル(率直)に考えればすむところを複雑に捉えてしまい、みずからドツボにはまり問題の解決をみずから迷宮入りにしてしまうことと類似(similar, analogous)である(幽霊の正体みたり枯れ尾花、負けの99%はこのような自滅による負けだと言われている)。
我々人間としてはなるべく、直観・幾何学・野性的にモノゴトを捉えたい。座標系の設定法(モノの観方、考え方、捉え方、発想の仕方、世界観)はかくも多様で、かくも本質的かつ決定的に重要なのである!!!!
(例)朝顔やつる状の植物は竿のうえを測地線(常螺旋:じょうらせん)にそって伸びてゆく。山登りも測地線にそって進めば体力の消耗を抑えられる。
(参考文献) 富岡礼子,曲がった空間の幾何学,講談社.
Heal the world(Michael Jackson)
(以上、徳川家康の遺訓)
昔から残っている古典的なものとか,自分から発信されていくもので構成すれば古さはでない(尾田栄一郎)
このとき、周囲の人間がつくる(能)力の(関数)ベクトル(の集合、ベクトル場)と自分自身の(能)力の(関数)ベクトルの内積(による正射影)が(並進一致(団結)で極大化する)お互いの間の評価(報酬)を与え合う。他方でまた周囲と自分自身が邂逅(かいこう、出会いのこと)して、何らかのコミュニケーション・リンク(およびそこで働く超偉大なるテンション(超万有引力!))が構築できればその相対位置ベクトルと周囲/自分自身の(能)力ベクトルとの外積が(作用・反作用で)お互いの能力の(関数)ベクトルにもたらす(直交で極大化する)力のモーメント(トルク)を与え合い、これはお互いにとって(運動)ポテンシャルエネルギに向上(活性化)をもたらす(なんと、驚くべきことにただ単に人と交流しているだけであってもその人の運動ポテンシャルエネルギーは向上しているというのだ!)。
異なる分野,学問,文化が交差する場では邂逅(かいこう、出会いのこと)して、何らかのコミュニケーション・リンクができれば互いに力のモーメントを与え合って活性化するうちにいつの間にか既存の概念が既存の枠を超えて組み合わさり,化学反応を起こしながら(たまたまうまい具合に)融合することで時に新しく非凡なアイディアが数多く生まれ,創造性が爆発的に開花して、イノベーションへと結びつくことがあるという。
これをフランス・ヨハンソンは『メディチ・インパクト(エフェクト)』と名付けた。ここで上記の『たまたま』は異なる分野,学問,文化が交差する場が確率的に生み出したある種の(統計学的)必然とでも言うべきものであろう(謙遜なのか成功者ほど、大数の法則にもとづいて『たまたま』がもたらす『必然』の効果・効用について自身の経験談をもとに説く傾向があるようだ)。
『メディチ』とはフィレンツェの実質的な支配者として君臨したメディチ家のことである。大富豪のメディチ家が各地からさまざまな芸術,文化,科学の突出したタレントを結集して交流を図ったことにより,異なる分野,学問,文化がバチバチと化学融合反応する場が生まれた。
USA for Africa - Harry Belafonte Tribute
(超一流の豪華ミュージシャンたちによる自然発生的なコーラスの協奏。音楽の楽しさの起点・原点を感じさせる)
Cyndi Lauper Solo Recording We R the World 1985
(超一流の豪華ミュージシャンたちがあーでもない、こーでもないといいながらすばらしい曲にアレンジしてゆくセッション。すばらしいモーメントの掛け合いの数々。固有値(熱量)、固有(関数)ベクトル(空間)のぶつかり合いによって生じる科学融合反応(イノベーション)。われわれの研究チームもこうありたい!)
Cyndi Lauper canta en aeroparque / performs at buenos aires airport
What a feeling
(フラッシュダンスの主題歌)
この、化学融合反応の連鎖・連環がタレント達にとって互いにさらなる(運動)ポテンシャルエネルギの向上(活性化)をもたらし、非凡かつ革新的なアイディアが数多く生まれ,爆発的な創造性の開花によるルネッサンスの勃興(ぼっこう)につながったのである。
(例)ルネッサンス期の画家は遠近法を解析することで、(ユークリッド面外の)無限遠点においてではあるが、平行線 が交わると合理的に捉えうる世界観に到達した(この詳細については射影幾何学について学ぶ必要がある)。平行な線路が地平線のはるか彼方で1点に集まるのをイメージとして見ているとき、われわれは射影幾何学的な(水平線たる)無限(遠直線)の一端を垣間見ていることになる。
(参考文献)イアン・スチュアート,川辺治之訳,無限,岩波科学ライブラリー,2018.
われわれは医療・バイオ分野においてITおよびロボット技術を基盤として『メディチ・インパクト(エフェクト)』のような大いなる革新をもたらそうと企図(きと)する(
Me-DigIT効果)。
このような大いなる革新(イノベーション)には、常に摩擦がつきものであるが、これを恐れてはならない!というのが、われわれのとるべき立場(stance)である。Sparkling wineよろしく、バチバチとした摩擦(sparkling)が種火(たねび)となって心にボッと火が灯(とも)る。摩擦あるところに、イノベーションやときめき(spark joy)も産まれるのだ!
運命の女神は勇者に微笑む(羽生善治の座右の銘)
上記の(運動)ポテンシャルエネルギの向上(活性化)を内積により自身の固有(関数)ベクトル空間へと正射影することで自分自身の人生の最終目的地に向かう推進力へと上手(巧み)に転換することを考えよう!このためには、自分自身の人生を全(まっと)うするための軸のみならず、周囲の人間の人生を全(まっと)うするための軸やこれらが集積してつくる力のベクトル場をしっかりと把握しておくことが肝要である。
彼(かれ)を知り己(おのれ)を知れば百戦殆(あや)うからず。彼を知らずして己を知るは一勝一負(いっしょういちぶ)す。彼を知らず己を知らざれば戦う毎(ごと)に殆(あや)うし。(孫子)
周囲(の人間)を巻き込んで、時間と手間ひまをかけて実力を最大限発揮しうる自分にとって最高の土俵(研究分野・領域)をこしらえ、独自の得意技(コア技能・技術)を鍛錬・洗練しつづけ、自分の土俵と独自の得意技で勝負する勇気・気概をもつ(自分の土俵をつくって、そこで相撲をとれ!!他人の土俵では相撲をとるな!!孫子の兵法)。
すなわち、自身が極限値たるカリスマ(絶対王者、アイドル)となるような人間部分列の仕組みを土俵としてこしらえて、できうるかぎりそこで相撲をとるように誘導すれば良いのである!
いかに自分の土俵をこしらえて、その土俵の上にフォーカスを持ってこれるかこそがわれわれの腕の見せ所なのであり、戦う前においてすでに勝負は99パーセントついてしまっているのである!フォーカスが自分にとっての土俵の外にもってゆかれてしまった時点で、ある意味、戦う前にすでに負けていると言えるのである、、、
数学者には数学者の、医学者に医学者の、ロボット工学者にはロボット工学者の土俵がある。さらに言えば、ひとりひとりにはそれぞれ独自の土俵がある。その土俵上の問題へといかに問題を抽出・分解・再構築(構造化)して落とし込んでゆけるかがわれわれの腕の見せ所であろう。
そうして、専門の土俵のうえではやはり、その独自の土俵のうえで日々鍛錬することで身につけてきた力士としての慣性(質量)・粘性・剛性と独自の必殺技(プロの世界観)がモノを言うのである!
(例)ブール代数によればp⇒qという命題において、前提の命題p(土俵設定)が間違ってしまっていると、すべての命題qはどんな命題であっても『意味のない真』になってしまう。土俵設定はかくも重要なのである!
(例)幾何学(もちろんトポロジーをも含めて)をハンドリングするとき、対象として何次元空間をハンドリングしているのか?という土俵設定をいつもしっかり・くっきり・はっきりとさせておかなければならない。
(参考文献)都筑卓司, トポロジー入門, 講談社, 2019.
当たり前のことかもしれないが、同じ空間内の2つ以上の線形独立(あるいは線形従属であってもよい)な(たとえば運動量pの)ベクトルは、もしリンクしてつながれば必ずなんらかのモーメント(角運動量ベクトルL=r×p)を互いに与え合う(作用反作用の)関係にあるという意味において潜在的な相互関係をもって存在している。
(例)2つの歯車がかみ合えば、(回転軸が平行であっても、平行でなくても)互いに(作用・反作用の力の)モーメントを与え合う。
つまり2つ以上の(関数)ベクトルが同じ空間内にそれぞれ独自の方向性(固有(関数)ベクトル)と大きさ(固有値)をもって(縮退せずにそこに)存在しているということ自体に必ず何らかの意味があると言えるのである(2つの(関数)ベクトルが平行であっても意味はある)!このことはIoTがもつ破壊的イノベーション力をみても納得がゆくであろう、、、
評価(内積)も(運動)ポテンシャルエネルギの向上(外積)も、お互いにお互いを認め合い、高めあってゆければそれに越したことはないのだろうが、一方でこのために羅針盤(らしんばん)たる自分自身の人生を全(まっと)うするための軸をブレさせてしまっては本末転倒というものであろう。
なぜなら、人生を全(まっと)うするための軸のブレはみずからの心の鏡に歪みを生じさせてしまうものだしまた、みずからの心身に大きな疲労と消耗を強いてしまうものだからである。
自分自身の人生を全(まっと)うするための軸が大きくブレずに、なおかつ(運動)ポテンシャルエネルギが向上して推進力も適度に得られる±(180-60=)120度※くらいまでの間で周囲との均衡を保ちながら力強くしなやかに、陽気(ポジティブかつゴキゲン)な人生を全(まっと)うするための航海を、(周囲の評価を気にすることなく)あせらずマイペースで断続的(intermittently)に進めてゆければ理想的なのだろうが、なかなかそううまくもゆかない、、、
※一般的に、サーボ系の安定余裕の目安は以下とされている。
ゲイン余裕:10~20[dB]
位相余裕 :40~60[°]
(参考文献)
https://detail-infomation.com/bode-plot/
http://arduinopid.web.fc2.com/N16.html
なぜなら周囲の(関数)ベクトル場(環境やそのboundary conditions)もまた、諸行無常で時々刻々と(initial conditionsから)変化してしまうものだからである。それもまた人生(の妙味)というものなのであろう(参考:
バタフライ効果)。
川の流れのように(美空ひばり)
ここで、正しいか正しくないかによって行動することは中長期の人生レベルで観たときにはあまりオススメできない。なぜなら、正しいかどうかもまた、諸行無常の言葉のごとく、永遠不滅のものではなく、時代、場所、集団、社会、周囲の状況によって柔軟(いとも簡単)に変化・変容してしまうものだからである。
たまたまその場にその時存在したから、誰か他人が定めた、ときに息苦しいと感じるローカルな拘束(制約:せいやく)条件がみずからの行動に課されるのである。そうして、このような拘束条件はグローバルに見たときには実に馬鹿げたものであったり、ものごとを進めるうえで大きなハンディになりうるものかもしれないのである!
このため、正しいか正しくないかによって行動することはブレ(迷い)につながり、ブレる軸には遠心力が働いてしまい、組織であれば、その組織は求心力(centripetal force)を失って簡単に自滅・崩壊してしまう。
本質は高周波ではなく、低周波成分にこそ現れるのである!そうしてそれらはsparseにmodelingされうる!すなわち、直観的(幾何学、野性的)に見通し良く単純・明解でありうる。
ブレ(迷わ)ないためには自分の人生の起点・原点と最終目的地をまずは定めるべきである。そうすれば、自分の人生に固有のベクトルが定まる。それが自分の人生に固有のシャンゼリゼ大通り(固有(関数)ベクトル空間)であり、あなたは心の中に折れることのない一本の槍を宿したことになる!
上記の自分の人生を全(まっと)うするための固有(関数)ベクトルに応じて定めた自分自身の人生を全(まっと)うするための固有軸(人生レベルでの価値・評価基準)に照らし合わせて、矛盾なく、なによりも自分自身が納得できるかどうかという価値観->世界観->信念(->執念)によって行動するべきであろう。すなわち自分自身の咀嚼(そしゃく)・嚥下(えんげ)する能力を信じて行動するべきであろう。
他人の意見(を自分軸で評価することもせずにただ単に鵜呑(うの)みにすること)で(生命の神髄(クイントエッセンス)にもとづく)自分のほんとうの心の声(自分軸)を消してはならない(Steve Jobs)
→自身の人生に固有の、折れることのない重い心の槍を持て!重心低く、ブレてはならない!
君の魂の中にある(生命の神髄(クイントエッセンス)にもとづく)英雄(人生を全うするための固有(関数)ベクトル空間、群・イデアル・体、土俵(上の技の集合)たるHeroの道)を放棄(abandon)してはならぬ。
どんな状況であれ(Under no circumstances)、
自分を卑下(despise)することなかれ。 気高くあれ(Be noble、人生を全うするための固有値を高めよ)。
我々の心に宿す神性(divinity)は、 (人生を全うするための固有(関数)ベクトル空間が)絶える(縮退する)ことのない不滅の存在(constant & immortal being)である(ことを我々自身に要求する)。
魂の中にある神(の道)を見定めよ(Determine the god in your soul)。
(Friedrich Wilhelm Nietzsche)
Hero (Mariah Carey)
人間の教養とは野性・野能を失うことではなく、(知性・知能とのコミュニケーション・リンク生成によって生命の神髄(クイントエッセンス)たる)野性・野能を(変容・)洗練(・進化)させることである(知性・知能とのコミュニケーション・リンク生成による野性・野能の変容・洗練・進化法)。
岡部伊都子
数学というものすごく厳密な学問においてさえ、究極のところ正しいか正しくないかは直観(幾何学、野性)的信念に頼らざるを得ない(玉野研一, なっとくする無限の話, 講談社)
Some times life, some times life is gonna hit you in the
head with a brick. Don't lose faith. (Steve
Jobs,ときとして人生では頭をレンガで殴られるような事態に見舞われます。信念を失わないでください。)
たとえ、損になろうが、周囲からクレイジーといわれようが(『You are too crazy !!!!』は研究者にとって最大のほめ言葉であり、『You too are crazy !!!!』と返すのが礼儀である!)、自分自身がやらずにはおられないことを迷うことなく信念(執念!?)をもって突き進み、ただやりきることに全身・全霊を注ぐのである!これにより人生から迷いを捨て去って、『不惑の人生』へと突入するのである!
The potential for these advances is thrilling──they could save and improve the lives of millions──but they’re not inevitable. They will happen only if people are willing to bet on a lot of crazy notions, knowing that while some won’t work out, one breakthrough can change the world. Over the next 100 years, we need people to keep believing in the power of innovation and to take a risk on a few revolutionary ideas. (Bill Gates)
このような進歩の可能性にはワクワクします。何百万人もの命を救い、生活を改善できます。しかし、必ず実現するとは限りません。このような進歩を起こすには、全部はうまくいかないけれども、たったひとつのブレイクスルーによって世界は変えられると確信しながら、たくさんのクレージーな考えに喜んで賭けないといけません。イノベーションの力を信じ、革命的なアイデアに賭けるべきです。次の100年間に我々が必要としているのは、それをやり続けられる人です。(ビル・ゲイツ)
天才とは僅(わず)かに我我と一歩を隔(へだ)てたもののことである。
同時代は常にこの一歩の千里であることを理解しない。
後代は又この千里の一歩であることに盲目である。
同時代はその為に天才を殺した。後代は又その為に天才の前に香を焚いている。
(芥川龍之介)
怠らず 行かば千里の 末も見ん 牛の歩みの よし遅くとも
(坂 静山)
決してブレない軸は上記の不動点や固有(関数)ベクトルとして、不動明王の如く、ありがたい存在であり、とっても魅力的な存在であることから、その効果のひとつとして周囲の人を惹きつける(attract)求心力(centripetal force)を有している。これは大木が鉛直上向きに伸びるときに周囲から栄養を吸収したり、川が流れるとき周囲から水を吸収するのに運動(幾何)学的に類似である(力線や流線を描いてみよ!)。
静中動(せいちゅうどう)あり、動中静(どうちゅうせい)あり
(例)アインシュタインの一般相対論によれば、質量の存在は宇宙空間に重力(引力)とよばれる勾配(曲率、ゆがみ)をもたらし光路すら引っ張り、曲げるモーメントを有する。そうしてこの重力(引力)によって星々はネットワーク構造(銀河系:ぎんがけい)を形成する。人間(じんかん)という宇宙空間においてもこれは同様であろう。
さらに質量を有する物体が(軸対称ではない)運動をすると、 上記の時空(空間)のゆがみが光速で伝わるというのである。これが重力波とよばれているものの正体である。重力波はすべてを貫通し、減衰しないといわれている。電磁波と重力波との違いは『振動するもの(=変位するもの)』である。すなわち、電磁波では空間そのものは振動せず、その中において電界と磁界のみが振動するものと捉えるのに対し、重力波では空間そのものが振動(伸び縮み)しているものと捉える(宇宙を3次元球面と仮定した場合)。
(例)ニューラルネットワークよろしく、学習によって得られる重み(質量)はネットワーク(空間)に勾配(曲率)をもたらす。脳のなかに宇宙と同じ『ネットワーク(空間)の重み(質量)と勾配(曲率)』の構造が見いだせることはきわめて興味深く、けっして偶然ではあるまい。そうして上記のネットワーク構造には、ラムゼイの定理によるイノベーション効果がその背後に潜んでいるのである!
すなわちまず、自分自身がやらずにはおられないことを軸として大きく育てる(その固有値たる質量を高める)。つぎにその結果としての求心力という重力(引力)を発生させることで、それが周囲から受ける(支持してもらえる)という(理想的な)流れをもつくってゆくことが可能になるのである。
~~~~~~~(仏教の世界観)
ロボットの先端効果器のみをただ漠然と眺めているだけではだめで、全体を補間してつなげてみなければロボットの運動の本質は理解できまい。ヒトの運動を理解する場合も同様であろう。迷ったら、いつでも、どこでも、何度でも最もプリミティブかつシンプルな起点・原点・出発点(starting point)・一丁目一番地となる原理・原則・定義・公理・機能・特(属)性・メカニズムにまで立ち返って行動、構成/構築論的により良いモデル・型・枠を求めて発想しなおすことが問題解決の近道である(急がばまわれ)。
提案するコンセプトを説明するときも同様である。なぜ(Why)、そのように(How)に発想したのか?どのようなプロセスをたどれば成功に至りうるのか?普遍的かつシンプルな原理・原則・定義・公理・機能・特(属)性・メカニズムを背景や起点・原点・出発点(starting point)・一丁目一番地、根本(根拠)に据えたうえで基礎・基盤・土台・土俵(infrastructure)をこしらえて、これを踏まえたうえでコンセプトの具体的かつ最終的な根幹枝葉花(果)実(こんかんしようはなかじつ)のイメージを簡潔かつ明瞭な形で視覚化、誰がみても一目瞭然の、より解かりやすい直観的な形で見せる(アフォーダンスを高める)。
世界観(神経ネットワークでつながれた目と手と脳に宿るモデル、型、枠)をうまく共有することができれば、周囲からの納得、理解、支援も得られやすいであろう。百聞は一見に如かず(Seeing is believing)、人間は目に見えるものを信じ込む習性(しゅうせい)をもっているのである。コンセプトの核をなしうる機能(関数)のつながり(フレームの構造)、アルゴリズムの流れ(フロー)などをビジュアル化して、専門用語を極力使わずに、直観・幾何学・野性的に分かりやすい形で見せるのだ。
最終目的からバックキャストして時間軸で相分割された中間目標を設定する(友人より)。
これだけはどんなことがあってもやらずにはおられないと思えるほど惚(ほ)れ込める研究対象を見出して、これに打込み、なおかつ、それが周囲から受ける(支持してもらえる)という(理想的な)流れをつくる。この流れをうまくつくれるかどうかが研究開発プロジェクトリーダー(あるいはマネージャー)の腕の見せ所であろう。
“If you build an army of 100 lions and their leader is a dog, in any fight, the lions will die like a dog. But if you build an army of 100 dogs and their leader is a lion, all dogs will fight as a lion.”
— Napoleon (1769 - 1821)
(伝える)~~~~~~~
よく伝わる(迫真の)演技をするための下準備として、役者は与えられたセリフや動作の入出力応答に対して整合性が合うように演じる対象のバックグラウンドやプロファイルを想像して作りこんだり、セリフのひとこと、ひとことに対して頭のなかで具体的な情景を思い浮かべてイメージしながら言葉を発する訓練をするという。さらに、これを支える本気と情熱は良く伝わるための必須の要件であり、その結果としての迫真の演技には人々の心を震わせ、感動させるモーメントが宿る。
プレゼンの説得力を高めるうえでもこのような伝わる(迫真の)演技のための訓練は大いに効果的といえるだろう。上記の入出力応答は整合性(つじつま)さえあっていればよく、途中の経路は問われないので、役者(の個性)によって変化しうる。この経路をいかに発想しうるかが、役者の腕の見せ所と言えるだろう。
~~~~~~~(伝える)
今、目の前に映っている像(ニーズ,シーズ,etc.)を時間軸・空間軸・人-物間(じんぶつかん)軸にまたがる、ある全体を構成する一断面(断片)として大局的に捉えうる世界観が重要。
(痛み・不安・恐怖・怒りの仮想フロベニウス根の仮想挿入による制御・抑制法)~~~~~
疼痛(とうつう)を研究している分野では痛みを評価するために、『痛みスケール』というものが定義されていて、自分がこれまでに感じた最大の痛みを基準として今現在自分が感じている痛みを規格化するそうだ。
痛みだけでなく、不安、恐怖、怒りといったものはいずれも、今現在われわれが抱えている最大の痛み、不安、恐怖、怒り(これを我々は痛み、不安、恐怖、怒りの最大固有値とそれに対応する固有(関数)ベクトルと呼ぶ)に対して必要以上に過剰なフォーカス(ベクトル)を向けがちである。しかしながら、この過剰なフォーカスはわれわれの精神にとって百害あって一利なしである。
なぜなら、痛み、不安、恐怖、怒りに対する過剰なフォーカスは精神を大きく蝕(むしば)み、われわれに与えられた有限の時間・経済・エネルギーを大きく消耗してしまうものであるからだ(これは自分の小指をくりかえし一生懸命ハンマーでたたいているようなものであり、精神的な自虐行為にほかならない!)。
痛みは怒り・恨みといった情動を巻き込んで記憶され、学習されるものらしい。これを踏まえてわれわれは『怒り・恨みの情動は決して学習・記憶するべきものではない!』という立場をとることとする。なぜならこれらは苦痛に変化してしまい自らを一生苦しめてしまいかねないものからだ。
また、より大きな痛み、不安、恐怖、怒りが入ってきた瞬間にそれまで抱えていた『最大の痛み、不安、恐怖、怒り』は一瞬でどこかに吹き飛んでしまう傾向があり、それまでの時間・経済・エネルギー投入はすべて無駄になってしまう性質(属性)のものである。
(例)医師から膵臓癌とつげられた患者はそれまで感じていた腰痛・肩痛といった痛みをすぐに忘れてしまうという。
そうしてその間に我々自身にとっての人生を全(まっと)うするための本質に対して十分なフォーカスが印加ができなかったことによる損失がいかに大きなものであったかということを、われわれはこれまでの手痛い人生経験のなかから、すでにうすうす感づいてしまっている。
すなわち、仮想的な最大固有値(線形代数学で言うところのフロベニウス根)に相当する痛み、不安、恐怖、怒りを仮想的に挿入してあらためて捉え直すことで今現在われわれ自身が抱えている痛み、不安、恐怖、怒りはなんと、抑え込むことができる性質(属性)のものであったのである(痛み・不安・恐怖・怒りの仮想フロベニウス根の仮想挿入による制御・抑制法)!!!!
もしそれが、3ヶ月(半年)たってもどうしても消えないような頑固でしつこい痛み、不安、恐怖、怒りであるのならば、それらはわれわれの人生にとって本質的な不安、恐怖、怒りというべきものであり、なんらかの抜本的な対策が必要かもしれないが、、、
そうではなくたとえばそれが、『自分にとって大切な人を喪失する痛み、不安、恐怖、怒り』が入ってきた瞬間に吹き飛んでしまうようなレベルの痛み、不安、恐怖、怒りであるのならば、それらは意識的にコントロールして押さえ込むことができる性質(属性)のものであり、またされるべき性質(属性)のものであろう。
すなわち、今この瞬間に抱えている痛み、不安、恐怖、怒りを、これより大きなあらたな仮想的な最大固有値(フロベニウス根)に相当する痛み、不安、恐怖、怒りを仮想的に挿入して抑え込んだうえで、フォーカス(ベクトル)を自分にとっての人生を全うするための本質(人生を全うするための骨格を形成するフロベニウス根とその固有(関数)ベクトル、言わば『心に宿した折れることのない一本の槍』)へと一刻もはやく意識的に転換することで、痛み、不安、恐怖、怒りによる余計な時間・経済・エネルギーの損失(loss)を極力抑える。一切は心に従って転ずる!
すなわち、心に宿した折れることのない『西遊記』に登場する如意金箍棒(にょいきんこぼう)の如(ごと)き一本の槍には(なんと!)痛み、不安、恐怖、怒りを抑え込む効果もあるのだ!
なぜならそうすることによってのみ、われわれは自身に与えられた固有の、内実がぎっしりと詰まった間隙や穴のない完備(complete, 甘美)な『真実の人生』を生きることができるからだ!
眼の前の大波は 確かに高き波なれど いつか消えゆく波なれば
その奥底に潜む真実の 人生にこそ力注がん!
~~~~~(痛み・不安・恐怖・怒りの仮想フロベニウス根の仮想挿入による制御・抑制法)
(関数)ベクトルを2つもつ。ひとつは長いスパンの最終目的地へと向かう、ブレを抑えるための(関数)ベクトル(人生を全うするための骨格を形成するフロベニウス根とその固有(関数)ベクトル、言わば『心に宿した折れることのない『西遊記』に登場する如意金箍棒(にょいきんこぼう)の如(ごと)き一本の槍』)。もうひとつは、周囲の状況と折り合いをつけながら日々葛藤、更新する中継地点への目標(関数)ベクトル。
人生を生き抜くには、中長期の将来ビジョンを踏まえて最終目的地へとむかうブレのない平衡点の軌跡(人生を全うするための中立軸)を設定して、これに極力正接するように(to be tangent)日々の目標(関数)ベクトルを維持・調節しながらも(曲がった空間のなかで曲率ゼロで真っ直ぐ進む測地線(そくちせん)のごとく!)決して折れることのないしなやかさをもって日々の出来事に柔軟(flexible)対応することが必要となろう。朝顔や植物のつるは曲がった空間である竿(さお)のうえを測地線にそって最短経路で真っ直ぐ進む(この曲線を常螺旋(じょうらせん)という)。飛行機の航路(大圏航路)、獣道(けものみち)、臓器の運動、登山道も同様である。(急がば常螺旋に沿ってまわれ法)
スコープ(何を、いつまでに、どこまでやるのか?)を決める。
こうしたいという自身あるいは周囲の欲求にもとづく小さな改善(イノベーションの欠片)の積み重ね(積分)』をイノベーション(過程)として捉え、大切にする。一般に理想的なソリューションを最初から追い求めるよりも、制約があるなかでひとつでもより多くの活動をこなしながら、すこしでもよりよいアイディア、よりよいソリューション(イノベーションの欠片)を生み出そうとするほうが有効であるからだ。
あらゆる局面で北極星や羅針盤(らしんばん)となる固有値・固有(関数)ベクトルはなにか(何が起点や原因となって核をなしうるものごとで、それらがどのようなバックボーン(指向性・方向性)をもって存在しているのか?およびそれらの相互作用、つながりはどうなっているのか)?
自分自身のバックボーンと局面のバックボーンはベクトルとして、どのような内積をもって世界(空間)に存在しているか?方向性の違いは45度、90度より大きいか小さいか?
方向性が45度を超えてくると同じひとつの集団としてまとまるのは困難になってくるし、方向性が90度を超える人たちからのアドバイスにはマイナス1を掛けて反面教師として受け取るなどのテクニカルな工夫が必要であろう。WhyとHowを常に意識しておくことが肝要。
起点・原点や原因(Why)を突きとめることが、原因から結果への流れやその拡がり(How)、バリエーションを理解することにつながるからだ。人の書いたプログラムを読むときだって、実装解は無数にあるが、重要な本質は考え方やコンセプトの核をなしうる基底となる起点・原点としての数式およびそのつながり(フレームの構造)、アルゴリズムの流れ(フロー)だ。
志定まれば気盛んなり。
(吉田松陰、安倍晋三首相の座右の銘)
志は気の師(すい)なり(孟子)。
熱い気持ちを周囲にぶつけてみる。
千日をもって『鍛』とし、万日をもって『錬』とする。
根気よく、絶え間なく周囲をEncourageする。
自分が納得できるところまでとことん突き進み、やりきる(つなげる)ことが大事。やりきってみた(つなげてみた)結果たとえその効果が有効でないという結論が得られたとしても、その結論は実際にとことん突き進み、やりきってみなければ(つなげてみなければ)決して得られなかったであろう、かけがえのない貴重な結論であり、とことん突き進み、やりきったことによる大きな成果と言える。
また、とことん突き進み、やりとげる過程で派生して(分岐して)得られた知見が思いもよらないものと結びついて、大きな成果に結実しうる、そういう価値観->世界観->信念(conviction)(->執念)をもつことが後々良い結果につながる(アポロ計画法)。
この仕事ができるか?と聞かれたら、『はい、もちろんできます』とまず答えよ。そのあとで懸命にそのやり方をみつけよ(そしてとことん突き進め!)(セオドア・ルーズベルト第26代アメリカ合衆国大統領)。
研究分野におけるシーズ(コア技能・技術、たとえば、機構・制御・画像処理、さらにはこれらを至適(してき:Acceptable)化、好適(こうてき: Favorable)化、最適(さいてき:Optimal)化するための人工知能・機械学習アルゴリズムか)に精通し、これを踏まえて応用分野(たとえば,医療・福祉)における、ニーズの開拓を行なう。また、ニーズを踏まえてコア技能・技術を改良、必要ならば新規開発することで研究分野を発展させてゆく。
医療ニーズの開拓とシーズ技術の開発は車の両輪(相補・連環的)。シーズとニーズは連環してゆく(あるいは橋渡しすることで連環させてゆける)という価値観->世界観->信念(->執念)をもつことが肝要。
一見バラバラに見えてもすべてはつながって(連関して)いる、あるいは将来つながる、あるいはつなげてゆくことができる(時間・空間・人-物間で働く、偉大な超万有引力の力を信じる)。そういう価値観->世界観->信念(->執念)をもつことが重要。
これまで繋がっていなかったものを繋げることで(超偉大なる)コミュニケーション・リンク(超万有引力)による相互モーメントや化学融合反応が発生し、その帰結・成果として『繋がれたものが新たに本質(フレーム)化』することがまさにイノベーション(の過程)そのものだと言うことができるからだ。北陸新幹線で金沢と東京が2時間半で結ばれれば、(結果として)これにともない人の流れも(本質・本格的に)大きく変わるのだ。
科学のどの進歩にも完璧な無知からはじまって、証拠にもとづく部分的な知識が(超万有引力的!につながって)しだいに確実になるという段階を経て、事実上確実になるという段階に至るという(複利的)変遷が含まれる(Howie)。
自分の専門領域以外の異分野のニーズとシーズ技術をフォロー・時期を捉えてマッチングしてつなげてゆくことが重要(日経新聞、日経産業新聞、日刊工業新聞、ニューズウィークが有用)。
I find out what the world needs, then I proceed to invent it (Thomas Edison).
世の中には数多(あまた)の謎・仕組みが埋め込まれている。これには際限がない。
A cube cannot be divided into the sum of two cubes. A quadruplet cannot be divided into the sum of two quadruplets. In general, when a power is greater than 2, that power cannot be divided into the sum of two powers. Regarding this theorem, I found a truly surprising proof, but this margin is too narrow to write it. (Pierre de Fermat)
立方数を2つの立方数の和に分けることはできない。4乗数を2つの4乗数の和に分けることはできない。一般に、冪(べき)が2より大きいとき、その冪乗数を2つの冪乗数の和に分けることはできない。この定理に関して、私は真に驚くべき証明を見つけたが、この余白はそれを書くには狭すぎる。 (ピエール・ド・フェルマー)
上記のフェルマーの最終定理はその単純・明解さにもかかわらず、オイラーはじめ歴代の天才数学者をもってしてもなお解決されずにいた。またそのことによってますますその存在感は増し、結果として永(なが)きにわたり数学の発展における原動力の一つであり続けた。アンドリュー・ワイルズが谷山–志村予想の一部を証明したことによってようやく最終的な解決に至るのだが、それは360年もの時が流れた1995年のことであった。
時間・空間・人-物間のモノゴトをつなげて本質を観ようとすることが解を考えるうえでの第一歩である。
研究は絵を書くのに似ている。何度も上書きをくりかえすことで研究の質の向上を図る。
著作・構築物やその作成・構築プロセスを通して人々を感動させたい!
他人のコピーをするのではなく、啓発されながらも自分のなかにある独自の価値観、世界観、ならびに信念(・執念)に立ち向かい、これを表現する。その結果としてたとえコピーと同じものが生成されたとしても、その構築(生成)プロセスはコピーによる生成過程とは質からして全く異なるものであり、時間軸・空間軸・人-物間軸上において大局的に考えてみれば進化・成長・発展性において上記の2つは似て非なるものと説得力とともに言い切ることができる。なぜなら、時間軸・空間軸・人-物間軸においたときのバックボーンはひとつひとつ異なるものだからだ。
誤解は極力解消するよう、フォローアップを極力行なう。理解される努力をして支持される流れ(の場,field)をつくる。基礎・基盤・土台・土俵・infrastructureの形成こそが重要である!戦う前においてすでに勝負は99パーセントついてしまっているのである!
---
整理・整頓・清潔
リーダーシップのみならず,フォロワーシップの能力もみがく。フォロワーシップは率先して応援団になることが重要。
優れたリーダーの共通項は,メンバーのことを心から気にかけて,彼らの成長と成功を願う人であること.さらに言えば,率直で誠実で楽観的で人間性にあふれている.
大丈夫、心配するな、なんとかなる!(一休宗純)
今のありのままを受け入れて、ありのままの自分として○○する(井上貴之)。
リーダーの役割は,目標とそれを達成することの意義をメンバーに示し,全員の気持ちを一つにして、目標達成を主導し、最終目的地に導く。どのような人にどのような支援を得たいかを明確に発信する。
メンバーから決断を求められたら,自らの意思と責任において決断を下す.間違っても,『多数決で決めよう』などと言い出してはならない。
『リーダー教習所論』
職場はリーダーにステップアップしてゆくための教習所という側面がある.考え,行動した結果に誤りがあっても,臆することはない.上司が部下の成長を促したいと考えるならば,あなたの挑戦を必ずサポートしてくれるはずだ.
Management is doing things right, leadership is doing the right things.
自分のビジョンを持ち,自分で決断するという姿勢を大事にする.
理念・志・戦略・戦術をもつ。
われわれの研究グループはアンメットメディカルニーズに応える医療機器を世界中の一人でも多くの方に提供できるよう,医デジ化の様々な可能性を追求し,医療機器等の研究開発を主導・推進する。
優れた判断,あるいは少なくともブレのない判断は,個人の,強い,明快な信念や価値観に基礎をおいて行なわれるものであり,それが決断につながる.
(ジャグディシュ・N・シース,アンドリュー・ソーベル)
情報(日経新聞、日経産業新聞、日刊工業新聞、ニューズウィークが有用)にも文脈(フロー,ストックなどの構造)があり,これがわかれば未来を見通すこともできる.
ある情報を得たければ,これに関連する情報をみずから発信する.情報は発信源に集まる(エコーの原理).
中心極限定理の主張:
おおくの互いに独立な確率変数の和として与えられる確率変数は,たとえ和に寄与するひとつひとつの確率変数の詳細はわからなくても,これらの独立な確率変数が多くなればなるほど,性質のよくわかったある確率変数に近づいてゆく.
(友人より補足)中心極限定理が成り立つのは人間間の相互作用が無視できる場合に限られる。その場合、平均値はゼロ、標準偏差は1/sqrt(n)である。
ところが実際の人間集団では集団思考という相互作用が働く。つまり、自分が集団の中心から外れるのを恐れる結果、よく考えずに誰かの意見に飛びつく。すると平均値はゼロでなくなり、標準偏差は1/sqrt(n)よりさらに小さくなる。これが自発的対称性の破れである。
正しいか,正しくないかではなく,矛盾なく説得力のある説明ができることを目指す(正しいかどうかを証明することは困難であり,悪魔の証明).
やらないことを決める(選択の本質).なにが自分にあたえられた使命か?自身の固有値,固有(関数)ベクトルを意識する.
自分は自分になるために生まれてきたのであって,それ以外の何物でもない.
自分がなりうる/行ないうる最高をめざす.
自分がなりうる最高の研究者となるためにはどうすればよいかを考える.
自分が行ないうる最高の研究をするためにはどうすればよいかを考える.
行けるところまで行きたい,行き着けるところまで行きたい(森田明夫先生).
自分が限界だとおもうことと,本当の限界との間にはまだ結構な差がある.われわれが狙うべきはその隙間だ.
(もうダメだ)助からないと思っても(実際は)助かっている(友人より).
どんな事でも「よかった」と思うことにしています.そうするとほんとうに「よかった」という結果になるから不思議です(ひろはまかずとし).
あらゆる意味でタフになる.タフ力増強.
プライドは高く、太く、強いものが好ましい!箸のようにぽっきり折れてしまうプライドではなく、ビールジョッキのように折れないプライドをもつべき!これは心の持ちようで何とでもできる!プライドを傷つけようとする相手には、サルがまた吠えている、、、くらいの気持ちで接するのがちょうどよい(まともに取り合うのは百害あって一利なしである)。
厳しさにさらされないと選手は育たない(耐性をもつウイルスになれ!).
困難にぶち当たっても、
立ち向かうことが人生でもっとも大切なことだとおもう.
運命の女神は勇者に微笑む(羽生善治の座右の銘).
ピンチはチャンスを背負ってくる.逆もまた真なり.
チャンスはピンチの顔をしてやって来る.
最悪の状況には必ず相応のチャンスが眠っている.
自信を積み上げながらも謙虚さを忘れず,リスクを恐れず新たな技術も取り入れながら過去の自分を乗り越える.
謙虚な姿勢を忘れず,人に誠意を尽くして,柔軟さをもつ.
(人間謙虚さ・誠実さを忘れるとロクなことがない、、、謙虚さ・誠実さを失っている時が人生の下り坂なのだろう、、、)
玲瓏
音が澄んで響くさま、透き通った美しさを示す言葉.
(羽生名人の好きな言葉)
両方から物を見ないと正しいものの見方はできない.
立場が変わると見える世界が変わり,価値観→世界観→信念(→執念)も変わる.
まず,相手の立場から観て,つぎに自分の立場からも観る.
視野(角)をあと30度ひろげてみよう。遠くを見たときに大きな(面積の)差になってくるはずだ。(牛田享宏先生).
(製品がユーザに)届くまでをきちっとデザインして、そこまでの責任を取ることを『つくる』ってことにしよう!(キングコング西野)
後悔しても,過ぎ去った時間が戻ってくる訳ではありません.
ミスをした現状を受け止め,つぎにすべきことはなにか?前向きに考える.
(渡辺 明)
苦しいときほど,登り坂(小泉匡永の座右の銘).
ここぞというときには逃げない.
背中をみせることも重要.
立場によらず信念(意志と実行力)さえあれば,だれでも道は開ける.熱い気持ちを周囲にぶつけてみる.(伊藤 阿耶雄)
人間,図太くないといかんで!
2乗で考える.
ありえることは起こる.ありえないと思うことすら起こる.
見たくないものは見えない,見たいものが見える.
可能な限りの想定と準備をする.
全ては変わる,変化に柔軟に対応しないといけない.
神は賽を投げない.ゴッドハンドは匙を投げない.
自身を客観視する.
あきらめなければ,目の前に無限の可能性がひろがる.
天才とは努力を続けられる人のことであり、それには方法論がある.
当時の棋士としてはもっとも多くの情報(最先端の棋譜)を持ち,もっとも多くの研究をしていたのが大山康晴(有吉道夫)
偶然をつかむということはすごく大事なこと.
何でやれるかというと楽しいから.
立ち止まることがもったいない.
反省なんかしないで,とにかく動いてほしい.
そうすればその分チャンスとの接点が増えるわけですから.
(樋渡啓祐)
心・技・体を尽くして応対・会話する.
以心伝心.心と心で対話する.
綸言汗の如し(りんげんあせのごとし)とは,皇帝が一旦発した言葉(綸言)は取り消したり訂正することができないという中国歴史上の格言.
All the world's a stage and all the men and women merely players.
この世は舞台,人はみな役者(シェークスピア)
『ひとつきっちりとした見せ場があれば,あとはどうとでもできる』あとはもう自分が楽しくやって,できれば読者も楽しませられたらいいなというスタンス(尾田栄一郎).
個性は批判される勇気をもたないともてない.
普通のことが,普通にできている有難さを忘れないようにしたい.
物事は精通すればするほど,応用の自由度が高まる.
学問を学ぶ姿勢としては,まずは鑑賞して楽しめる状態をめざす.どの学問にも,その学問のエッセンスを凝縮したような珠玉のトピックスは存在する.まずは,これを鑑賞して味わい楽しむことからはじめる.
(数学などの)理論に関しては,最初から厳密さを意識すると,勉強するのも億劫になってしまうので,まずは,みずからが矛盾なく納得・ひとに矛盾なく説明できることを目指す.
証明したいことの否定に矛盾がないかどうかも検討してみる価値がある。
美しさ(対称性)をまず考える.
美しいモデルにヒッグス粒子による外乱が働いて現実世界ができている.対象なモデルから(が)対称でない現実世界ができる(を創る).
簡単で興味のあるものごとからせめてゆく.慣性の法則を利用.
数学では、特別な場合から証明してこれを一般・抽象化.
抽象的な概念を理解するときは具体的な対象を考えながら理解をすすめることが有効。
why 抽象的な概念は、基礎となる具体的な対象(例)をかならず持っている。
特殊相対論(1905)→一般相対論(1916)
率直な数学的表現が物理の本質を垣間見させる⇒率直な数学的表現が人生の本質を垣間見させる
想像力にもとづく創造力→疲れを知らない
他方,
受動的→理解できない些細なことに大して必要以上に執着しがち→行き詰まり,疲れる
想像力をフルスロットルにして,論文や本のなかの図を眼で見て,理解したら,読み飛ばすくらいの姿勢でちょうど良い。理解できない些細なことにはできるかぎり執着しないのが吉(よし)。書いている本人すら理解できていない可能性もある。
Believe yourself !
自分を信じる.
Force makes right.
力は正義なり
完全な善もないし,完全な悪もない.
We are right, because we have the power.
成長戦略は作文で終わらせず実行こそ大事(桑原智隆)
いつやるの?今でしょ!(林 修)
『できる,できない』ではなく『やるか,やらないか』が大切
やりたいことをやらないのは一番体に悪い(ジャイアント馬場).
アドレナリンの善用こそ人生の妙薬.
好きな研究に打ち込まないでいるのは,好きな研究に対する背信行為.
好きなことに一生懸命に打込むことが物事を好転させる.
部分的には悲観しながらも,全体的には楽観すべき
(立木義浩)
失敗から学び,つぎにつなげてゆくことが大事.挑戦のないところに失敗もない.失敗がなければ,学習することも,自分を成長させることもできない.失敗は成功につながる,あるいはつなげることができるという価値観->世界観->信念(->執念)をもつ.
失敗(エラー)することには耐えられるが、挑戦しないでいることには耐えられない。成功を学ぶためにはまず、失敗(エラー)(の構造)を(プロセスとして)学ばなければならない。人生でなんども失敗(エラー)してきた(。もちろん、現在も新しい挑戦をしつづけているのだから当然、失敗しつづけている、その継続的なプロセスの集積がある)からこそ私は成功した(/つづけている)。(マイケル・ジョーダン)
いい結果に目がいきがちだが,倍以上の失敗がある.
(イチロー)
Even a mistake may turn out to be the one thing necessary to a worthwhile achievement. (Henry Ford,失敗とは,よりよい方法で再挑戦する素晴らしい機会である)。
かつての成功体験にまどわされることなく、成功したからと言って、同じことを繰り返していてはダメだ.数多く獲得したメダルよりも(試合に勝てなかった)9回の『ノー・メダル』が次へのメダルにつながっている.
室伏広治
終わりのないトンネルはない!
努力は必ず報われる.うまくいかなかったら,努力が足りなかったんだと考える.そのうえで,なにがなんでもという気持ちをもつ(小宮山 悟).
待っていれば全てがやってくる.ただし,懸命に努力しながら待っていればの話だけどね(トーマス・エジソン).
旨い話の裏には辛い日々、眠れない夜、それから継続的にやってくる失敗と挫折がいくつもある。成功までの道のりは長い。本当に長い。多くの場合は、長過ぎる。
どんなに人生が台無しになっても、どんなに辛くても、自分の情熱に従って、その旅路を楽しんだほうがいい。
まず可能な範囲でResponseを早めることを考える(第1のResponsibility).そのうえで内容のクオリティを高めることを考える(第2のResponsibility).
人間の能力の差は「知っているか,知らないか・早いか,遅いか」だったりする.
いくら鳶が鳴いたからといって,天日の歩みが止まるものではない.
時間だけは,平等に,着実に過ぎてゆく.
祈願(希望)は他人のために行なう(する).期待は自分にかける.
地震がいつおこるかはわからないが、最大の被害はハザードマップで想定できる。
ポアンカレは数学的発見のプロセスを①準備、②培養、③啓示の3段階に分けた。
①準備:十分に意識を働かせて問題に没頭し、行き詰まること
②培養:無意識がそれを熟考している間、じっと待つこと
③啓示:頭の中で小さな電球が灯って、あの有名な『エウレカ!』の瞬間(moment!)が訪れること!
あなたたちはいかなる競争の場面になって、世界のどこにいようとも負けることはないでしょう。そういう厳しい訓練を受けてきました。しかし、競争に勝つということは相手を負かすことではないことを肝に銘じてください。相手もまた勝っていてもいいのです。厳しい競争の中で闘うバランス感覚を忘れないでください。
明日の勝利の為に今日負けれない人は最終的には敗者となる
→明日の成功のために,今日失敗できない人は敗者となる
→失敗か、成功か?という考え方ではなく、失敗は成功という全体の一部である!という考え方でゆくのがよい。
http://www004.upp.so-net.ne.jp/silverfox/CCP019.html
トイレのときは蛇口を捻(ひね)るところもあらう。
ごみはなるべく拾う。
メラビアンの法則
言葉:聴覚:視覚=7:38:55
YCUのグローバル教育
地球規模的な発想をもち,世界をひとつの市場として捉えて将来を見据え,持続可能な社会をつくっていくために活躍できる人材が社会から求められている.
具体的に社会人基礎能力として
①実行力
②課題発見・解決力
③発信力
④ストレスコントロール力(耐性)
⑤コミュニケーション力
⑥語学力
⑦人間関係構築力
グローバル人材とは
国内外を問わず,いかなる場面や環境であっても柔軟に能力を発揮できる人材,つまり,
自分の考えを相手に伝える力と相手の考えを受け入れる力の双方を兼ね備えた人材.
めざすべき対話力:
①おかれている状況に応じて,相手の文化的背景や立場をふまえて話を聞き,
②聞いたことを理解し,これに関して,本質の抽出・分解・再構築をおこない,
(再構築は付加価値をつける過程でもあることに着目されたい)
③自分の意見を説得力があるかたちで,効果的に相手に伝える.
(伝えるべきことの核心を3つにまとめる,なぜなら,3は人間の頭が扱いやすい数だから)
クリエイティブな人はココがちょっと違う!22の違い
革新に必要なもの
①大志、
②遂行する腕力、
③実現のためのリーダーシップ
ストレス解消法
Sports
Travel
Rest
Eat
Sleep
Smile
少人数の人間のさまざまな能力を足し合わせたとき,そのグループ全体としてどんな力を発揮するかはいろいろ違ってくる.だが,百人,千人,あるいは何万人という大人数の人間のさまざまな能力を足し合わせたときには,グループ全体の力は概ねお決まりのものにしかならない(中心極限定理より)
関西学院大学のスタディ・スキル・セミナー
①起立・礼
②周りを見る,社会では観察力が大事
③「読む・書く・話す・聴く」の学ぶ力をつける
④文章術の基本.文頭はひとマスあける,句読点の打ち方
⑤論理的な話し方,問題点→解決策
⑥聴く態度
⑦要約する技術,2分間で自分の強みと弱みを話す
自分の強み:専門知識に基づく物事の再構築技術
弱み:注意不足によるミスが多い.
⑧学びが実社会で役に立つとわかれば,学生は必ずやる気を起こす.
素人発想,玄人実行(金出武雄先生)
プロとしての技術と知識を磨きつつ,「素人的」で素直な発想ができるか.
アベノミクス成長戦略(海外展開)
1. 食文化
2. 医療システム
3. 教育制度
4. 交通エネルギー
動向シナリオと行動シナリオを周囲と共有する
IT技術の発達にともない,人々の有機ネットワーク的な情報のやりとりが容易になり,情報が爆発的に($n!$的に)増加する時代に,今後,ビジネスなどもますますグローバル展開するように推察される.個人レベルであっても,そうなってゆくだろう.
このような時代に,機動的に対応してゆくために,社会動向がどのように変化していって(動向シナリオ),われわれはこれにどう対応するべきか(行動シナリオ)?
という動向および行動シナリオを周囲の人間とあらかじめコンセン
サスとして共有しておいて,いざというときに機動的に行動したいという,人々の要求も生まれてきている.
そこで,われわれも,周囲の人々とざっくばらんに意見交換するなかで,まず,10年くらいのスパンで世の中の起こりうるイベントや社会動向のながれを予
測するとともに,われわれなりの動向シナリオを形成・共有してゆければと期待している.
つぎに,動向シナリオが予想どおりにうまくはまれば,自分をふくめた周囲の人々が,有機的なネットワークとして,これに機動的に対応できるような,われわれなりの行動シナリオを策定・
共有してゆければと期待しています.可能であれば,受動的のみならず,能動的に国家や社会に提言してゆければおもしろい.
世の中は単純ではない(複雑だ!)→
すべて連環している連環系→正の,あるいは,負のスパイラル構造を有する→e^{\lamnda t}→どんどん悪くなるか,これを逆回転させるなんらかの方策を用いて改善するか?→連環学
(コラム)
連環学は,京大が2003年度から始めた新しい学問分野.以前は別々に研究されてきた森や海の生態系や人間との関わり(相互作用)について体系的に学ぶ.消化器系も連環系,各種臓器も連関系として扱うべき.細胞シートは微分形か,,,
岩波書店のキーポイントシリーズのコンセプト
①読者がもっとも知りたい疑問(問題点)や自信のもてない急所(難所)を選び,その攻略法(解決策)を明確に示す.
②何のためにこれを学ぶ(研究する)のか,学習(研究)の動機が学ぶ側(レフェリー側)の視点で,すっきりと理解できる.
③例題(サブ課題)形式の構成で,各ポイントの課題と目標(マイルストーン)を明確にしながら,解説する.
④直観的にわかりやすいイメージ(図表)を大切にして,数学(研究)理解のコツが得られる.
⑤『試験の問題がとける』という自信が身につく→研究のご利益を説く.研究分野や市場に与えるインパクト・波及効果・市場規模など,なるべく具体化(数値化)しておく,,,
グローバル人材とは
①行動的
②積極的
③失敗を恐れない
④好奇心が旺盛
⑤国籍を問わずコミュニケーションがしっかりとれる
⑥知識だけでは弱い
⑦海外経験
パラメータを2個変えたものを比較してはいけない
7月6日の読売新聞の記事にあった、
すこしsentimentalな気持になった記事、、、
以下抜粋、、、
童話『ごんぎつね』の児童文学者、新美南吉が安城高等女学校の教員時代に作成した英語のテストが見つかったという。学生時代を過ごした花の都を懐かしんでだろう。<日比谷公園につれていってもらえますか?>。解答のほうを示せば、そういう英文和訳の設問があった。「・・・に連れていってもらえますか?」と独り言をいってみたい場所は、誰にでもあるだろう。子供の頃に暮らした町のように、何もかもが変わり果てて、記憶のなかだけに景観をとどめている場所もある。<廃駅をくさあぢさゐの花占めてただ歳月はまぶしかりけり>(小池光)。雨の音を聴きながら記憶を旅する夜も、たまにはいい。


































![{\displaystyle {\mathcal {Z}}[x_{n-k}]=z^{-k}{\mathcal {Z}}[x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/889002e7427023e17c6778bb41e8b8b6f60c73db)









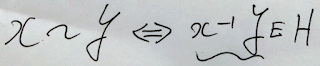











 ,
, 












![{\displaystyle {\begin{aligned}\Gamma (z+1)&=\int _{t=0}^{\infty }{t^{z}(-e^{-t})'}\,dt\\&=\left[-t^{z}e^{-t}\right]_{t=0}^{\infty }+z\int _{t=0}^{\infty }{t^{z-1}e^{-t}}\,dt\\&=z\Gamma (z)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ca0d996dec7a0da6e85ba7cf1a22fa352c71760)







